7. Feature Engineering

Unser Ziel ist ein Datensatz, der pro Zeile eine Beobachtung über ein Objekt enthält, das es zu analysieren gilt. Jede Beobachtung ist durch eine Menge von Features beschrieben. Eine sinnvolle Auswahl der Features ist entscheidend für eine gute Analyse.

Mit Hilfe von Feature Engineering erzeugen wir gute Features. Das Thema ist sehr groß und wir können hier nur auf einige Beispiele eingehen. Diese sind teilen wir in drei Kategorien ein:

• Encoding: ein bestehendes Feature wird in eine für das Analyse-Verfahren/den Machine Learning Algorithmus geeignetere Form gebracht, z.B.

  • Binning: einteilen von Skalarwerten in Intervalle, z.B. Einteilung der Startjahre von Liniennetzen in Epochen (z.B. vor 1900, 1900 - 1914, …)

  • One-Hot-Encoding: für kategorische Features wird ein einzelnes Feature je Kategorie gebildet, z.B. statt einer Spalte Alter mit Werten “alt”, “normal”, “neu” werden drei Spalten mit entsprechenden Titeln gebildert - immer nur eine dieser Spalte enthält eine 1, der Rest ist 0

  • Skalierung: umrechnen numerischer Werte auf eine andere Skala, z.B. Normalisierung aller numerischen Spalten auf den Bereich 0 bis 1 oder logarithmische Skalierung eines sehr großen Wertebereichs

• Extraktion: es sind Rohdaten zu einer Beobachtung vorhanden, die nicht direkt in der Analyse verwendet werden können. Per Algorithmus können nützliche Features aus den Daten generiert werden, z.B.

  • Kalenderdatum: Jeder Tag existiert nur ein mal und daher sind keine Muster ableitbar. Aus dem Datum sind jedoch Features ableitbar, die eine gute Aussagekraft besitzen können, z.B. Wochentag, Feiertag (ja/nein), Tage bis Ostern, …

  • Bilder sind im ersten Schritt nur große Arrays von Farbwerten. Abgeleitete Features können beinhalten: Metadaten (Größe, Ort der Aufnahme) oder Bildinhalte, z.B. per Neuronalen Netz ausgewertet wie viele Bahnsteige es auf einem Foto eines Bahnhofs gibt

  • Aus Texten können Strukturinformationen, das Vorkommen oder die Häufigkeit von einzelnen Wörtern und weitere Informationen abgeleitet werden

• Anreicherung: es sind weitere Datensätze vorhanden aus denen Information zum betrachteten Objekt abgeleitet werden. In unserem Beispeil betrachten wir die Liniennetze von Städten und haben im ersten Schritt nur wenige Informationen (Stadtname, Land, Koordinaten, Gesamtlänge). Über weitere Datensätze können wir z.B. anreichern:

  • Anteil der verschiedenen Transport-Modi (z.B. Bus, S-Bahn, Strassenbahn) an der Gesamtlänge

  • Anzahl der Haltestellen und deren durchschnittliche Abstände

  • Anzahl der Linien

In diesem Kapitel werden wir einige dieser Beispiel umsetzen. Auf Kalenderdaten gehen wir explizit im nächsten Kapitel ein. Für eine tiefere Behandlung von Feature Engineering siehe z.B. das Buch “Feature Engineering for Machine Leanring” von Zheng und Casari [ZC18].

INFO

Die Übungen und Beispiele basieren auf Daten über weltweite Systeme des öffentlichen Nahverkehrs von https://www.citylines.co

Wir laden zuerst wieder die Standard-Bibliotheken und unser cities-DataFrame:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

cities = pd.read_csv('data/cities_non_zero.csv', index_col='id')
cities.head()

	name	country	lat	long	start_year	age	length_km
id
11	Athens	Greece	37.966667	23.716667	1867	157	86.834
139	Boston	United States	42.350000	-71.083333	1806	218	615.505
206	New York	United States	40.783333	-73.966667	1817	207	1089.854
54	Helsinki	Finland	60.166667	25.000000	2017	7	0.639
231	San Francisco	United States	37.783333	-122.433333	1863	161	351.531

7.1. Encoding

Je nach verwendeten Analyse-Verfahren eignen sich bestimmte Formen besser oder schlechter, wir betrachten einige Beispiele.

Binning

Binning kennen wir schon von den Histogramm-Charts. Dabei werden numerische Werte in Intervallen zusammengefasst. Der entstehende Informationsverlust kann von Vorteil sein, um die Daten einfacher verständlich zu machen (z.B. für Charts/explorative Datenanalyse), Modelle zu vereinfachen (z.B. weniger Split-Möglichkeiten in baumbasierten Modellen) oder Rauschen/Messfehler/Scheingenauigkeiten aus den Daten herauszufiltern.

Die Methode pd.cut wandelt eine numerische pd.Series (Spalte) in eine kategorische mit den Intervallen als Kategorien. Neben der Series gibt es einen weiteren Parameter bins, der die Intervalle bestimmt, es gibt u.a. zwei Möglichkeiten:

• Ein einzelner Integer, der die Anzahl der Bins vorgibt, die alle gleich groß aus dem Wertebereich der Spalte gebildet werden

• Eine Liste von Zahlen, die die Grenzen der einzelnen Bins vorgibt. Aus einer Liste [1, 2, 3, 4] werden die Bins (1, 2], (2, 3], (3, 4] gebildet, wobei ( exklusiv und ] inklusiv bedeutet (Zahl ist nicht/ist Teil des Intervalls). Soll das erste Intervall links inklusiv sein ([1, 2] im Beispiel), dann muss der Parameter include_lowest=True gesetzt werden.

Optional kann noch mit dem Parameter labels eine Liste von Labels für die Intervalle angegeben werden. Weitere Parameter sind in der API Referenz cut. Siehe auch die API Referenz qcut, wenn die Bins basierend auf Quantilen gebildet werden sollen.

Im Folgenden wenden wir verschiedene Binnings auf die Streckenlänge an:

# Gleichmäßiges Binning in 10 Intervalle
cities['length_10_bins'] = pd.cut(cities['length_km'], 10)
cities.head()

	name	country	lat	long	start_year	age	length_km	length_10_bins
id
11	Athens	Greece	37.966667	23.716667	1867	157	86.834	(-4.131, 477.661]
139	Boston	United States	42.350000	-71.083333	1806	218	615.505	(477.661, 954.684]
206	New York	United States	40.783333	-73.966667	1817	207	1089.854	(954.684, 1431.706]
54	Helsinki	Finland	60.166667	25.000000	2017	7	0.639	(-4.131, 477.661]
231	San Francisco	United States	37.783333	-122.433333	1863	161	351.531	(-4.131, 477.661]

# Binning in exponentielle wachsende Intervalle
# Erst mal Intervalle festlegen
bins = [0] + ([2**i for i in range(14)])
bins

[0, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192]

# Labels festlegen
labels = [f'{lower} - {upper}' for lower, upper in zip(bins[:-1],bins[1:])]
labels

['0 - 1',
 '1 - 2',
 '2 - 4',
 '4 - 8',
 '8 - 16',
 '16 - 32',
 '32 - 64',
 '64 - 128',
 '128 - 256',
 '256 - 512',
 '512 - 1024',
 '1024 - 2048',
 '2048 - 4096',
 '4096 - 8192']

# Anwenden des Binnings
cities['length_exp_bins'] = pd.cut(cities['length_km'], bins, labels=labels)
cities.head()

	name	country	lat	long	start_year	age	length_km	length_10_bins	length_exp_bins
id
11	Athens	Greece	37.966667	23.716667	1867	157	86.834	(-4.131, 477.661]	64 - 128
139	Boston	United States	42.350000	-71.083333	1806	218	615.505	(477.661, 954.684]	512 - 1024
206	New York	United States	40.783333	-73.966667	1817	207	1089.854	(954.684, 1431.706]	1024 - 2048
54	Helsinki	Finland	60.166667	25.000000	2017	7	0.639	(-4.131, 477.661]	0 - 1
231	San Francisco	United States	37.783333	-122.433333	1863	161	351.531	(-4.131, 477.661]	256 - 512

# Binning nach Quartilen
cities['length_quartiles'] = pd.qcut(cities['length_km'], 4, labels=['Q1', 'Q2', 'Q3', 'Q4'])
cities.head()

	name	country	lat	long	start_year	age	length_km	length_10_bins	length_exp_bins	length_quartiles
id
11	Athens	Greece	37.966667	23.716667	1867	157	86.834	(-4.131, 477.661]	64 - 128	Q3
139	Boston	United States	42.350000	-71.083333	1806	218	615.505	(477.661, 954.684]	512 - 1024	Q4
206	New York	United States	40.783333	-73.966667	1817	207	1089.854	(954.684, 1431.706]	1024 - 2048	Q4
54	Helsinki	Finland	60.166667	25.000000	2017	7	0.639	(-4.131, 477.661]	0 - 1	Q1
231	San Francisco	United States	37.783333	-122.433333	1863	161	351.531	(-4.131, 477.661]	256 - 512	Q4

One-Hot-Encoding

Im vorherigen Abschnitt haben wir per Binning aus skalaren Werten Kategorien erstellt. Ebenso gibt es von vornherein kategorische Daten, wie z.B. der Transport Mode. Bei den “Linien” ist zwar eine numerische transport_mode_id gegeben, jedoch handelt es sich hierbei um Kategorien, da die Zahl an sich keine Bedeutung hat. Die Reihenfolge der Transport Modes hat ebenso wenig Bedeutung wie der numerische Abstand zwischen Transport Mode IDs. Zwei Transport-Modi sind sich nicht ähnlicher als zwei andere nur weil die numerische Differenz zwischen ihren IDs kleiner ist. Ähnlich verhält es sich in vielen Anwendungen mit Wochentagen, die nicht als kontinuierlicher Verlauf sondern als Kategorien zu interpretieren sind (Dienstag verhält sich anders als Mittwoch aber aus der Differenz Mittwoch zu Dienstag lässt sich nichts über die Differenz Samstag zu Freitag ableiten).

Viele Algorithmen interpretieren kategorische Spalten gar nicht oder falsch. Nehmen wir als Beispiel Wochentage bei einer linearen Regression:

• Wochentage als Strings kodiert “Montag”, …, “Sonntag”: kann nicht vom Modell verarbeitet werden, da es nur mit numerischen Inputs funktioniert

• Wochentage als Integer 0 bis 6 kodiert: impliziert einen linearen Verlauf der Zielvariable von Wochenanfang bis Ende. D.h. zum Beispiel bei einer Umsatzprognose, wenn rausgefunden wird, dass im Schnitt samstags der Umsatz um 25% höher liegt als montags, dann wird geschlossen, dass es mittwochs 5% mehr Umsatz als dienstags gibt)

Eine Lösung hierfür ist es für jede Kategorie die Zugehörigkeit als eigenes Feature zu interpretieren. Also z.B. ein Feature “Montag”, dass 1 ist für Montage und sonst 0, und ähnliche Features für die weiteren Wochentage. Zu beachten ist, dass pro Beobachtung immer nur eines der Features 1 ist und der Rest 0.

Dies Verfahren nennt sich One-Hot-Encoding und wird typischerweise im Rahmen einer scikit-learn Pipeline eingesetzt - dies werden Sie später noch kennenlernen. Einfach lässt sich es aber auch mit pandas umsetzen mit der Funktion pd.get_dummies. Anbei ein Beispiel, das die Intervall-Kategorien aus den Binning-Beispiel umwandelt:

pd.get_dummies(cities['length_quartiles']).head()

	Q1	Q2	Q3	Q4
id
11	0	0	1	0
139	0	0	0	1
206	0	0	0	1
54	1	0	0	0
231	0	0	0	1

pd.get_dummies(cities['length_exp_bins']).head()

	0 - 1	1 - 2	2 - 4	4 - 8	8 - 16	16 - 32	32 - 64	64 - 128	128 - 256	256 - 512	512 - 1024	1024 - 2048	2048 - 4096	4096 - 8192
id
11	0	0	0	0	0	0	0	1	0	0	0	0	0	0
139	0	0	0	0	0	0	0	0	0	0	1	0	0	0
206	0	0	0	0	0	0	0	0	0	0	0	1	0	0
54	1	0	0	0	0	0	0	0	0	0	0	0	0	0
231	0	0	0	0	0	0	0	0	0	1	0	0	0	0

Skalierung: Linearisierung

Verschiedene Modelle treffen verschiedene Annahmen über die Daten, die sie verarbeiten. Eine Annahme könnte sein, dass bestimmte Werte einer Normalverteilung entsprechen. Häufig setzen wir lineare Modelle, die eben lineare Korrelationen voraussetzen. Betrachten wir anhand einem Beispiel, was bei nicht linearen Daten passiert.

Wir generieren und plotten zunächst einen Datensatz, wo y eine exponentielle Funktion von x ist und addieren noch ein zufälliges Rauschen dazu:

# x: 50 zufälle Werte aus dem Bereich 10 bis 100
x = np.random.randint(10, 100, 50)
# y: ist eine expontielle Funktion von x und zu jedem y wird noch eine Zufallszahl addiert
y = 1.05**x + (20 * np.random.rand(50))
plt.scatter(x,y)
plt.show()

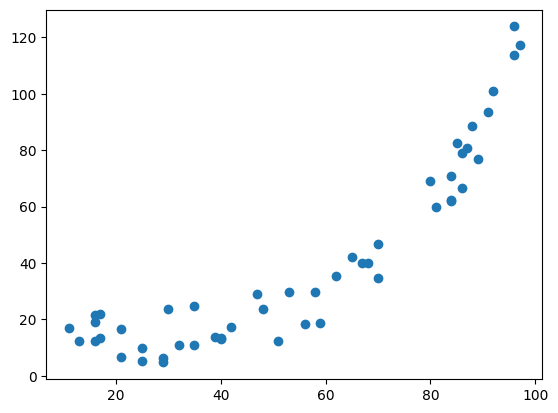
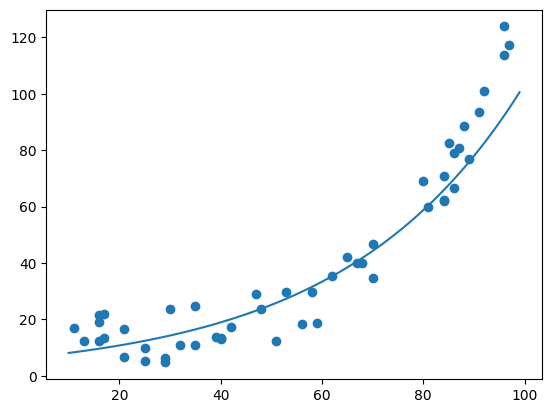
Wenn wir nun eine einfache lineare Regression anpassen, dann kann sie zwar den generellen Aufwärtstrend in den Daten erkennen aber vereinfacht den Datensatz zu stark:

# Lineare Regression
coeffs = np.polyfit(x,y,1)
# Berechne Regression für alle x aus Bereich 10 bis 100
x_lin = np.arange(10, 100)
y_pred_lin = x_lin * coeffs[0] + coeffs[1]
# Plotten der Regression und der Datenpunkte
plt.plot(x_lin, y_pred_lin)
plt.scatter(x,y)
plt.show()

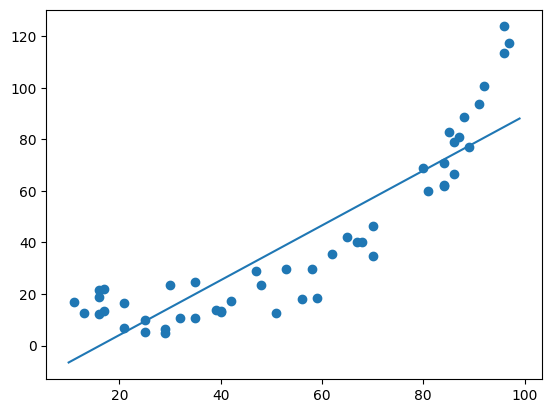
Wir müssen entweder auf einen komplexeren Algorithmus gehen oder wir transformieren die Daten so, dass der Zusammenhang zwischen x und y linear wird. Dies ist für uns einfach, da wir bereits wissen, dass es sich um einen exponentiellen Zusammenhang handelt und wir somit mit der inversen Funktion Logarithmus auf eine Linearität kommen.

# Linearisieren von y
y_log = np.log(y)
# Berechnen der Linearen Regression auf x und linearisierten y
coeffs_log = np.polyfit(x, y_log, 1)
# Vorhersage der linearisierten Werte:
y_log_pred = x_lin * coeffs_log[0] + coeffs_log[1]

plt.plot(x_lin, y_log_pred)
plt.scatter(x,y_log)
plt.show()

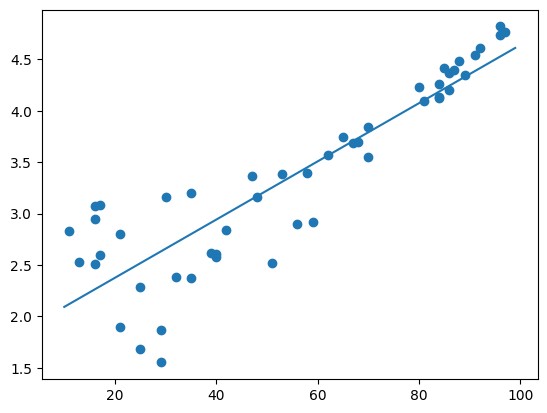
Wir können mit np.exp als Invertierung unserer Invertierung (np.log) wieder den ursprünglichen Wertebereich herstellen.

# zurückrechnen mit np.exp auf ursprünglichen Wertebereich (invertieren von np.log)
y_log_pred_exp = np.exp(y_log_pred)

plt.plot(x_lin, y_log_pred_exp)
plt.scatter(x,y)
plt.show()

Skalierung: Normalisierung

Einige Algorithmen erwarten, dass alle numerischen Features die gleiche Skala nutzen. Beispielsweise berechnet der k-Means Clustering Algorithmus die Ähnlichkeit zwischen Beobachtungen anhand der Differenz der einzelnen Feature-Ausprägungen. Der Algorithmus hat keine Möglichkeit zu erkennen, dass eine Differenz von 100 unterschiedliche Gewichtungen haben kann:

• Eine Differenz von 100 Jahren im Alter eines Liniennetzes ist ein beträchtlicher Unterschied

• Eine Differenz von 100 Metern in der Länge des Lininennetzes ist wohl eher zu vernachlässigen

Das einfachste Verfahren für geschlossene Wertebereiche ist 0-1-Scaling. Dabei wird jeder Wert auf eine lineare Skala zwischen 0 und 1 umgelegt, die den Wert ins Verhältnis zum minimalen und maximalen Wert der Spalte setzt. Dieses und weitere Verfahren sind sehr einfach in scikit-learn Pipelines einzubinden aber das 0-1-Scaling gelingt sehr einfach mit pandas:

cities['length_scaled'] = (cities['length_km']       - cities['length_km'].min()) /\
                          (cities['length_km'].max() - cities['length_km'].min())
cities.head()

	name	country	lat	long	start_year	age	length_km	length_10_bins	length_exp_bins	length_quartiles	length_scaled
id
11	Athens	Greece	37.966667	23.716667	1867	157	86.834	(-4.131, 477.661]	64 - 128	Q3	0.018069
139	Boston	United States	42.350000	-71.083333	1806	218	615.505	(477.661, 954.684]	512 - 1024	Q4	0.128897
206	New York	United States	40.783333	-73.966667	1817	207	1089.854	(954.684, 1431.706]	1024 - 2048	Q4	0.228336
54	Helsinki	Finland	60.166667	25.000000	2017	7	0.639	(-4.131, 477.661]	0 - 1	Q1	0.000000
231	San Francisco	United States	37.783333	-122.433333	1863	161	351.531	(-4.131, 477.661]	256 - 512	Q4	0.073559

Die 0-1-Skalierung behält die Gleichgewichtung von Differenzen über den gesamten Wertebereich einer Spalte bei, also z.B. werden die 100km Differenz zwischen 1km und 101km Streckenlänge genauso gewichtet wie die 100km Differenz zwischen 1000km und 1100km. Wenn dies nicht gewünscht ist bietet sich z.B. ein Quantil-Binning an:

cities['length_pctile'] = pd.qcut(cities['length_km'], 100, labels=np.arange(100)).astype('float') / 100.0 
cities.describe()

	lat	long	start_year	age	length_km	length_scaled	length_pctile
count	137.000000	137.000000	137.000000	137.000000	137.000000	137.000000	137.000000
mean	30.363248	-4.732200	1951.233577	72.766423	252.385190	0.052774	0.494818
std	26.016580	74.304119	63.454623	63.454623	521.966382	0.109422	0.291913
min	-38.957350	-123.100000	1806.000000	4.000000	0.639000	0.000000	0.000000
25%	27.950000	-73.583333	1890.000000	19.000000	31.236000	0.006414	0.240000
50%	40.450000	0.104970	1981.000000	43.000000	83.040000	0.017274	0.490000
75%	47.330404	16.333333	2005.000000	134.000000	248.289000	0.051916	0.740000
max	60.392500	151.200000	2020.000000	218.000000	4770.864000	1.000000	0.990000

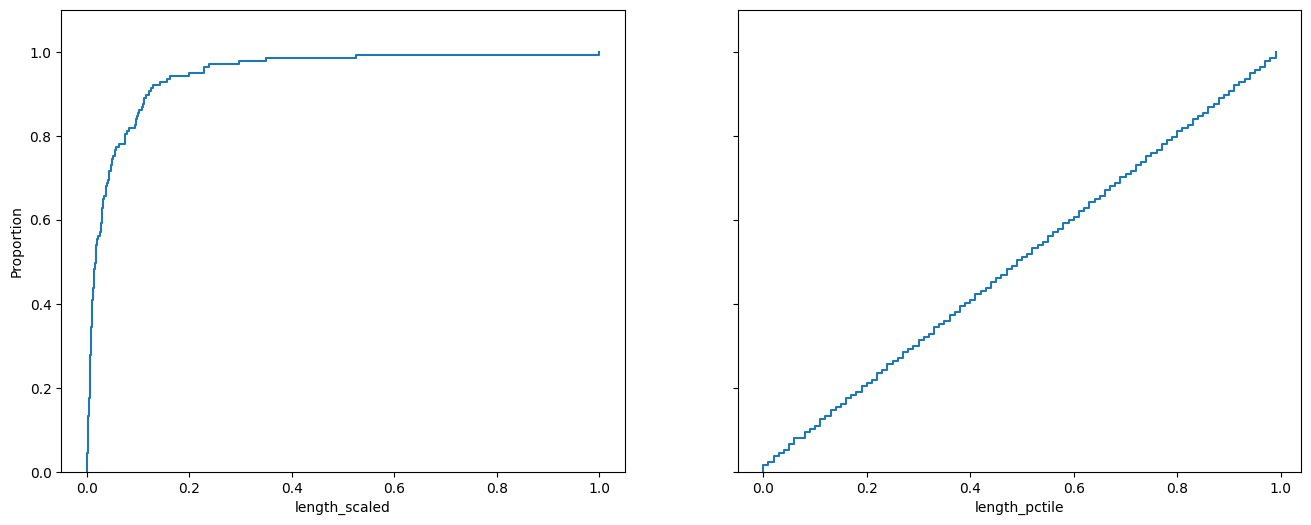
Beachten Sie die unterschiedlichen Durchschnitts- und Medianwerte in der vorigen Tabelle und die Werteverteilungen in den folgenden Charts:

fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(16,6))
ax1.set_ylim(0,1.1)
sns.ecdfplot(cities,x='length_scaled', ax=ax1)
sns.ecdfplot(cities,x='length_pctile', ax=ax2)
plt.show()

7.2. Extraktion

Für die Extraktion werden häufig komplexe Modelle eingesetzt, sozusagen als Vorberarbeitungsschritt bevor die eigene Analyse durchgeführt oder das eigene Modell trainiert werden. Dies ist insbesondere bei Bild-, Audio- und Textdaten der Fall. Einige dieser Verfahren werden wir beim Thema Modellierung/Machine Learning kennenlernen aber jeder der drei genannten Bereiche bietet genug Komplexität für eigene Kurse.

Auf das Thema Kalenderdaten gehen wir im nächsten Kapitel ein.

7.3. Anreicherung

In unserem Beispiel haben wir weitere Datensätze unter anderem zu Linien und Streckenabschnitten, die wir analysieren und auf Stadtebene agreggieren können bevor wir sie dann an unser cities-DataFrame per merge anbinden. Darüberhinaus könnten auch weitere Datenquellen angebunden werden, z.B. ein Daten aus Wikipedia (per Wikidata) zu Städten oder z.B. zu Kalenderdaten die historischen oder vorausgesagten Temperaturen aus einem Wetterservice.

Starten wir mit dem Datensatz über Transport-Modi aus dem letzten Abschnitt:

city_transport_modes = pd.read_csv('data/city_system_lengths.csv')
city_transport_modes.head()

	id	brt	bus	commuter_rail	default	ferry	heavy_rail	high_speed_rail	inter_city_rail	light_rail	people_mover	tram	total	name
0	8	0.0	0.0	0.000	0.0	0.0	42.100	0.0	0.0	0.000	0.0	0.571	42.671	Amsterdam
1	275	0.0	0.0	0.000	0.0	0.0	0.000	0.0	0.0	24.251	0.0	0.000	24.251	Angers
2	11	0.0	0.0	0.000	0.0	0.0	86.834	0.0	0.0	0.000	0.0	0.000	86.834	Athens
3	131	0.0	0.0	0.000	0.0	0.0	79.456	0.0	0.0	0.000	0.0	4.212	83.668	Atlanta
4	132	0.0	0.0	51.691	0.0	0.0	0.000	0.0	0.0	0.000	0.0	0.000	51.691	Austin

Wir wollen Features generieren, die die prozentualen Anteile von Bus und Bahnverbindungen zusammenfasst - ein Feature für den Restanteil lassen wir außen vor:

city_transport_modes['share_bus'] = city_transport_modes['bus'] / city_transport_modes['total']
# Bestimme alle Spalten mit 'rail' im Namen
rail_columns = city_transport_modes.columns.str.contains('rail')
# Summiere pro Zeile (also entlang der Spalten, axis=1) alle Spalten mit Rail im Namen
city_transport_modes['share_rail'] = city_transport_modes.loc[:, rail_columns].sum(axis=1) / city_transport_modes['total']
city_transport_modes = city_transport_modes[['name', 'share_bus', 'share_rail']]
city_transport_modes.head()

	name	share_bus	share_rail
0	Amsterdam	0.0	0.986619
1	Angers	0.0	1.000000
2	Athens	0.0	1.000000
3	Atlanta	0.0	0.949658
4	Austin	0.0	1.000000

Nun mergen wir die Daten basierend auf dem Städtenamen an unser DataFrame (und werfen für die Übersichtlichkeit ein paar der Längenbins raus):

cities = cities.drop(columns=['length_10_bins', 'length_quartiles']).reset_index().merge(city_transport_modes, on='name')
cities.head()

	id	name	country	lat	long	start_year	age	length_km	length_exp_bins	length_scaled	length_pctile	share_bus	share_rail
0	11	Athens	Greece	37.966667	23.716667	1867	157	86.834	64 - 128	0.018069	0.52	0.0	1.000000
1	139	Boston	United States	42.350000	-71.083333	1806	218	615.505	512 - 1024	0.128897	0.91	0.0	0.992650
2	206	New York	United States	40.783333	-73.966667	1817	207	1089.854	1024 - 2048	0.228336	0.95	0.0	0.992324
3	54	Helsinki	Finland	60.166667	25.000000	2017	7	0.639	0 - 1	0.000000	0.00	0.0	1.000000
4	231	San Francisco	United States	37.783333	-122.433333	1863	161	351.531	256 - 512	0.073559	0.78	0.0	0.928160

Fläche der Städte

# Cached version of https://data.heroku.com/dataclips/akipfiszptbqbwwwgtsqxufmjeur.csv
# Datum 19.07.2021
stations = pd.read_csv('data/stations.csv')
stations.head()

	id	name	geometry	buildstart	opening	closure	city_id
0	1703	Wanshoulu	POINT(116.288966863116 39.9062894419391)	1965.0	1971.0	999999.0	15
1	7694	Keisei Tsudanuma	POINT(140.024812197129 35.6837744784723)	1921.0	1921.0	999999.0	114
2	6003	Kossuth Lajos tér	POINT(19.0462376564033 47.5054880717671)	0.0	0.0	999999.0	29
3	7732	Saint-Charles	POINT(5.3801556 43.3024646)	1973.0	1977.0	999999.0	74
4	7695	Keisei Makuhari-Hongo	POINT(140.042146725175 35.6726021159981)	1991.0	1991.0	999999.0	114

# Unsere bekannte Extraktion der Koordinaten
coords = stations['geometry'].str.extract(r'(?P<long>[-+0-9.]+) (?P<lat>[-+0-9.]+)')
# Umwandeln in Float-Zahlen
coords = coords.astype('float')
# Zusammenfügen und in cities speichern
stations = pd.concat([stations, coords], axis=1)
# Gruppierung, um min/max für Long und Lat zu bekommen
city_area = stations.groupby('city_id').agg({'long': ['min', 'max'], 'lat': ['min', 'max']})
city_area.head()

	long		lat
	min	max	min	max
city_id
1	-60.568570	-57.902687	-35.578998	-33.889360
4	-71.211068	-70.524529	-34.170293	-33.085068
8	4.802912	4.989269	52.295586	52.402128
11	23.639791	23.944750	37.892695	38.073389
13	100.408210	100.751225	13.567731	13.989726

Nun haben wir die Koordinaten von einem zum Äquator parallelen “Rechteck” (die Erde ist eine Kugel), das gespannt werden müsste, um alle Haltestellen einer Stadt zu umfassen. Beachten Sie den Multi-Level-Index, der die Spaltennamen beschreibt. Um auf eine Spalte zuzugreifen müssen wir nun ein Tupel mit Spaltennamen für jedes Level angeben, z.B. city_area[('long', 'min')] um auf die erste Spalte zuzugreifen.

Um die Fläche zu berechnen müssen wir die Differenzen der Koordinaten in km umrechen - das ist nicht ganz trivial, da die Erde eine Kugel ist. Wir halten uns an die verbesserte Methode aus https://www.kompf.de/gps/distcalc.html

city_area['latd'] = (city_area[('lat', 'max')] + city_area[('lat', 'min')]) / 2 * 0.01745
city_area['width'] = 111.3 * np.cos(city_area['latd']) * (city_area[('long', 'max')] - city_area[('long', 'min')])
city_area['height'] = 111.3 * (city_area[('lat', 'max')] - city_area[('lat', 'min')])
city_area['area'] = city_area['width'] * city_area['height']
city_area.head()

	long		lat		latd	width	height	area
	min	max	min	max
city_id
1	-60.568570	-57.902687	-35.578998	-33.889360	-0.606111	243.859141	188.056706	45859.346942
4	-71.211068	-70.524529	-34.170293	-33.085068	-0.586803	63.629191	120.785517	7685.484683
8	4.802912	4.989269	52.295586	52.402128	0.913488	12.672873	11.858126	150.276524
11	23.639791	23.944750	37.892695	38.073389	0.662804	26.755428	20.111251	538.085126
13	100.408210	100.751225	13.567731	13.989726	0.240439	37.079394	46.968091	1741.548371

# Hinzufügen zu cities-DataFrame:
cities = cities.merge(city_area['area'], left_on='id', right_index=True)
cities.head()

	id	name	country	lat	long	start_year	age	length_km	length_exp_bins	length_scaled	length_pctile	share_bus	share_rail	area
0	11	Athens	Greece	37.966667	23.716667	1867	157	86.834	64 - 128	0.018069	0.52	0.0	1.000000	538.085126
1	139	Boston	United States	42.350000	-71.083333	1806	218	615.505	512 - 1024	0.128897	0.91	0.0	0.992650	13608.576647
2	206	New York	United States	40.783333	-73.966667	1817	207	1089.854	1024 - 2048	0.228336	0.95	0.0	0.992324	18648.863681
3	54	Helsinki	Finland	60.166667	25.000000	2017	7	0.639	0 - 1	0.000000	0.00	0.0	1.000000	11163.760947
4	231	San Francisco	United States	37.783333	-122.433333	1863	161	351.531	256 - 512	0.073559	0.78	0.0	0.928160	4376.967223

7.4. Feature-Selektion

Nach der Generierung einer großer Anzahl von Features stellt sich die Frage, ob diese alle für ein Modell/eine Analyse verwendet werden sollen oder ob eine Vorauswahl getroffen werden soll. Dies hängt unter anderem ab von:

• Größe des Datensatzes: erst bei einer großen Anzahl von Beobachtungen können wir viele Features verwenden - ansonsten wird der Raum der möglichen Ausprägungen nicht ausreichend ausgefüllt

• Algorithmus: manche Algorithmen können gut mit vielen Features umgehen und kümmern sich teilweise selbst um die Feature-Auswahl. Andere Algorithmen erzeugen wenig robuste Modelle, stolpern über korrelierte Features oder entwickeln enormen Rechenbedarf

• Rechenpower: bei großen Datensätzen mit vielen Features kann die Modellerstellung je nach Modell zu komplex für die verfügbare Rechenkapazität werden

Ein Ansatz ist die Korrelation, der verschiedenen Features untereinander und vor allem mit der Zielvariablen zu bestimmen, um Features auszuwählen, die gut mit der Zielvariablen korrelieren aber untereinander möglichst wenig korreliert sind. In unserem Beispiel haben wir keine ausgewiesene Zielvariable, können jedoch trotzdem die Korrelationsanalyse skizzieren:

cities.loc[:,'start_year':'area'].corr(numeric_only=True)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
/tmp/ipykernel_517/1113810736.py in <module>
----> 1 cities.loc[:,'start_year':'area'].corr(numeric_only=True)

TypeError: corr() got an unexpected keyword argument 'numeric_only'

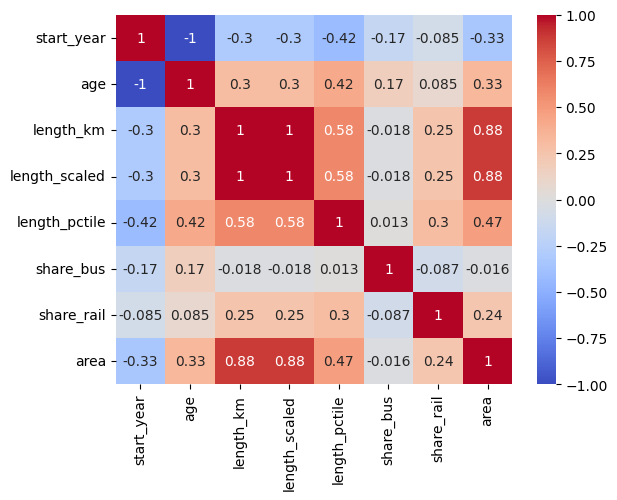
Einige Beobachtungen:

• Absolute Länge des Liniennetzes korreliert mit der Fläche

• Absolute und 0-1-skalierte Länge des Liniennetzes korreliert (per Definition) perfekt

• Längenperzentile korrelieren stärker mit dem Alter als die absolute Länge

• Korrelationen mit start_year sind genau gleich groß aber mit umgedrehten Vorzeichen wie bei Alter

Mit seaborn können wir die Korrelationen auch graphisch anzeigen:

sns.heatmap(cities.loc[:,'start_year':'area'].corr(numeric_only=True), annot = True, fmt='.2g',cmap= 'coolwarm')
plt.show()