2. Clustering#
Clustering-Verfahren gehören in die Gruppe der unüberwachten Klassifizierungsverfahren. Anhand der Features in einem Datenpunkt soll berechnet werden, welchen anderen Datenpunkten im Datensatz er ähnelt. Mit diesen Datenpunkten soll er dann in eine gemeinsame Klasse gefasst werden.
Beim Clustering können kleine Änderungen an den Parametern und die Auswahl des Algorithmus große Auswirkungen auf das Ergebnis haben. Es erfordert also immer Zeit für die Ergebnisprüfung und zum Experimentieren und ist üblichrweise nicht mit einem Methodenaufruf erledigt.
2.1. Identität als Lage im Raum#
Clustering-Verfahren suchen Ähnlichkeiten zwischen Datenpunkten, indem sie die Features der Datenpunkte als einen Vektor auffassen. Die Feature-Werte, die quasi die Identität des Datenpunkts darstellen, beschreiben nun die Lage des Datenpunkts im hochdimensionalen Raum: Ein Datensatz mit 50 Features beschreibt einen 50-dimensionalen Raum. Zwei Datenpunkte mit ähnlichen Werten für z.B. das 1. Feature liegen auf dieser Dimension des Raums nahe zusammen; sind die Werte sehr unähnlich, liegen die Punkte in dieser Dimension weit auseinander. Cluster sind nun Anhäufungen von Datenpunkten in diesem Raum – also Gruppen von Datenpunkten, die ähnliche Featurewerte haben.
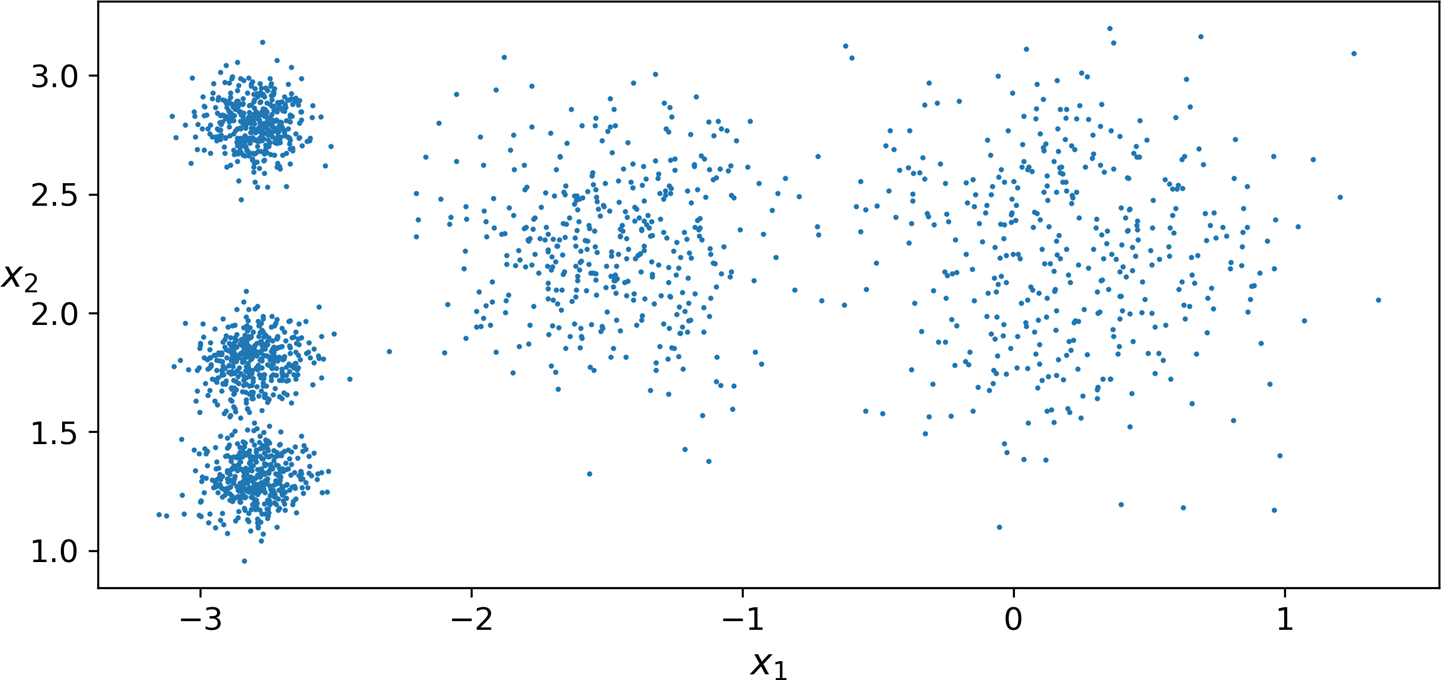Abb. 1: Cluster im zweidimensionalen Raum (Géron 2019)
Abb. 1 (aus Géron 2019) zeigt einen Datensatz mit zwei Features (x1 und x2). Im linken Teil sind drei kompakte Cluster zu sehen: Alle Datenpunkte haben einen ähnlichen Wert für x1 und sortieren sich anhand ihres Werts für x2 in die drei Cluster ein. Für jedes Cluster kann man einen Zentroiden als den Durchschnitt der am Cluster beteiligten Feature-Vektoren berechnen. Dies ist quasi ein typischer Vertreter des Clusters.
Der Raum in Abb. 1 ist einfach genug, dass wir ihn visuell erfassen und analysieren können. Im hochdimensionalen Raum ist das nicht mehr möglich; hier übernehmen die Cluster-Algorithmen.
2.2. Anwendungen#
Clustering verwendet man im Bereich der deskriptiven Datenanalyse zur Exploration. Es zeigt auf, welche Ähnlichkeiten zwischen Datenpunkten vorhanden sind und welche Featurewerte für die verschiedenen Sorten von Datenpunkten typisch sind. Hierzu betrachtet man die Featurewerte des Zentroiden. Betrachten Sie noch einmal die drei Cluster in Abb. 1, die sich nur im x2-Wert unterscheiden: Diese Dimension ist offenbar hoch informativ über die Datenpunkte, wenn x1=-2.9 vorliegt. Mit dem entsprechenden Domänenwissen kann diese Clusterbildung überprüft und interpretiert werden.
Manchmal weisen Cluster auch auf Fehler oder Artefakte der Datenerhebung hin; bei der Codierung von Wochentagen als Zahlen treten häufig ähnlich deutliche Gruppen auf (da es natürlich keinen Wert zwischen “Mittwoch” und “Donnerstag” gibt, die Codierung als z.B. 3.0 und 4.0 dies aber nahelegt). Ob diese Cluster relevant sind oder nicht muss wieder mit Hilfe von Domänenwissen entschieden werden.
Die identifizierten Cluster können auch zur Charakterisierung von neu aufgetretenen Datenpunkten verwendet werden. Wenn die Cluster z.B. verschiedene Kundentypen anzeigen, kann ein neuer Kunde aufgrund seines bisherigen Verhaltens einem bekannten Cluster zugeordnet und entsprechend angesprochen werden.
Aufgabe: Wie würden Sie die Zuordnung des Neukunden zum Cluster vornehmen?
Antwort:
Clustering kann auch zum Auffinden von Outliern verwendet werden. Das sind untypische Werte, die fern aller Cluster liegen. Es handelt sich entweder um fehlerhafte Datenpunkte (die man entfernen möchte) oder besonders informative Sonderfälle. Der einfachste Weg, sie zu identifzieren, ist die Berechnung ihres Abstands zu allen bekannten Cluster-Zentroiden. Ist der gefundene Abstand größer als für die anderen Datenpunkte üblich, handelt es sich um einen Outlier.
2.3. Wie es weitergeht#
Wenn Sie noch keine Vorkenntnisse zum Thema Clustering haben, arbeiten Sie die Theorie-Unterlagen zu K-Means-Clustering durch. Dies ist ein einfacher Standard-Algorithmus, der für die Exploration weit verbreitet ist. Bearbeiten Sie dann das Beispiel unten. Der Abschnitt “Weitere Algorithmen” ist für Sie nicht verpflichtend.
Wenn Sie K-Means schon kennen, können Sie die Theorie überspringen. Machen Sie dann bitte direkt beim Beispiel unten weiter und bearbeiten Sie danach “Weitere Algorithmen”.
2.4. K-Means: Theoretischer Hintergrund#
Der K-Means-Algorithmus erstellt Cluster, so dass der Gesamt-Abstand der Datenpunkte zum Mittelpunkt ihres Cluster (die inertia) minimiert wird. Es sollen also idealerweise Cluster entstehen, die kompakt sind, so dass alle Datenpunkte nah zusammenliegen. Ob dies möglich ist, hängt sehr von der Verteilung der zu clusternden Datenpunkte im Raum ab!
Zur Abstandsbestimmung wird das Euklid’sche Maß verwendet. Sie kennen es in seiner Grundform: \(a^2+b^2=c^2\). In unserer Situation sind \(a\) und \(b\) konkrete Featurewerte zweier Punkte (z.B. die Werte des 1. Features im Datensatz) und \(c\) der Abstand zwischen den Punkten. Da wir normalerweise sehr viel mehr als nur ein Feature haben, wird das Maß erweitert und für jedes Feature eine Summe der quadrierten Werte eingeführt. Aus dieser Abstandsberechnung folgt nun, dass Features, die sehr hohe Werte haben, in der Abstandsberechnung ein starkes Gewicht bekommen (\(100^2+100^2 >> 1^2+1^2\)). Deshalb müssen wir bei realen Datensätzen die Features skalieren, damit sie alle im selben Wertebereich liegen.
Neben der Kompaktheit der Features ist ein weiteres Kriterium für die Qualität des Ergebnisses ist die Anzahl der Cluster. Werden nur wenig Cluster gebildet, haben die einzelnen Instanzen logischerweise einen größeren Abstand zu ihrem Cluster-Mittelpunkt, als wenn es viele kleine Cluster gibt. Die Anzahl der zu bildenden Cluster ist bei K-Means allerdings ein vorgegebener Parameter. Das heißt, wir müssen üblicherweise verschiedene Cluster-Anzahlen ausprobieren, um einen guten Parameterwert zu finden.
Der K-Means-Algorithmus arbeitet iterativ so lange, bis sich die Clusterzuweisung der einzelnen Datenpunkte bzw. die inertia der Konfiguration nicht mehr ändert.
Abb. 2 zeigt einen kleinen Beispiel-Datensatz. Dieser soll in zwei Cluster getrennt werden.
Abb. 2: Ein kleiner Datensatz
Der Parameter für den Algorithmus ist also gegeben. Der erste Schritt ist das Wählen von zwei zufälligen Positionen für die Cluster-Zentren, die Zentroide. Diese werden dann in den weiteren Schritten verschoben, bis die Cluster konvergieren. In Abb. 3 sind die zufällig gewählten Zentroide rot markiert. Sie liegen offensichtlich noch nicht ideal.
Abb. 3: Zufällig gewählte Zentroide
Die folgenden Schritte werden bis zur Konvergenz (Cluster-Zuordnungen ändern sich nicht mehr bzw. inertia ändert sich nicht mehr) in einer Schleife wiederholt.
Alle Datenpunkte werden dem nächstgelegenen Zentroiden zugeordnet. Man verwendet z.B. das euklidsche Distanzmaß a^2+b^2 = c^2, generalisiert auf die benötigte Anzahl an Dimensionen. Dabei sind a und b die Differenzen in den Zellwerten der beiden Datenpunkte. Abb. 4 zeigt die ersten Cluster in unserem Beispiel.
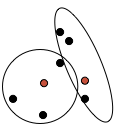Abb. 4: Erste Cluster entsprechend den Zufallszentroiden
Nun werden die Zentroide neu berechnet, sie haben also zum ersten Mal einen echten Zusammenhang mit den Daten. Neuer Zentroid eines Clusters wird der Durchschnitt aller Cluster-Mitglieder (der Zentroid ist bei K-Means also nicht unbedingt ein existierender Datenpunkt). Abb. 5 zeigt die berechneten Cluster-Zentroide.
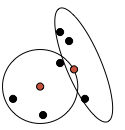Abb. 5: Aufgrund der Clustermitglieder berechnete Zentroide
Wir führen das Beispiel weiter: Jetzt wird Schritt 1 wiederholt und überprüft, ob sich jedes Clustermitglied noch im richtigen Cluster befindet oder ob es ggf. einem anderen Zentroiden näher liegt. Ist dies der Fall, wird es dem anderen Cluster zugeschlagen (Abb. 6).
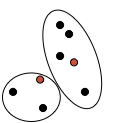Abb. 6: Neu berechnete Clusterzuordnungen
Aufgrund der ggf. neu zugeordneten Cluster-Elemente müssen die Zentroide neu berechnet werden (Schritt 2). Eine neuerliche Abb. 7 zeigt das Endergebnis des Clusterns. Die beiden Datenpunkte unten links sind in einem Cluster, alle andere im zweiten (mehr Cluster sind nicht möglich, da der Parameter k=2 vorgegeben ist).
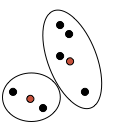Abb. 7: Endergebnis des Clusterns mit K-Means
Aus dem Beispiel ist ersichtlich, dass die Position der anfänglich gewählten Zufalls-Zentroide das Ergebnis stark beeinflusst. Hätte einer oben und einer unten im Raum gelegen, wären die finalen Cluster vermutlich anders eingeteilt. Diese Abhängigkeit von einem zufälligen Startwert gilt es bei K-Means zu beachten. Wir halten unsere Ergebnisse reproduzierbar, indem wir einen festen random_state mitgeben, der den generierten Zufall wieder aufrufbar macht (er ist damit nicht weniger zufällig!).
2.5. K-Means: Beispiel “Weine clustern”#
Wir spielen das Clustering von echten Daten anhand eines Beispiel-Datensatzes von scikit-learn (ursprünglich das UCI ML Wine Data Set) durch.
Wir importieren die Daten von sklearn. Sie finden ein Jupyter Notebook mit den im Folgenden beschriebenen Schritten unter scripts/modeling-clustering-kmeans.ipynb.
# Imports
from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn import metrics
# Daten herunterladen
wines = datasets.load_wine()
# Was haben wir bekommen?
print(wines.DESCR)
.. _wine_dataset:
Wine recognition dataset
------------------------
**Data Set Characteristics:**
:Number of Instances: 178 (50 in each of three classes)
:Number of Attributes: 13 numeric, predictive attributes and the class
:Attribute Information:
- Alcohol
- Malic acid
- Ash
- Alcalinity of ash
- Magnesium
- Total phenols
- Flavanoids
- Nonflavanoid phenols
- Proanthocyanins
- Color intensity
- Hue
- OD280/OD315 of diluted wines
- Proline
- class:
- class_0
- class_1
- class_2
:Summary Statistics:
============================= ==== ===== ======= =====
Min Max Mean SD
============================= ==== ===== ======= =====
Alcohol: 11.0 14.8 13.0 0.8
Malic Acid: 0.74 5.80 2.34 1.12
Ash: 1.36 3.23 2.36 0.27
Alcalinity of Ash: 10.6 30.0 19.5 3.3
Magnesium: 70.0 162.0 99.7 14.3
Total Phenols: 0.98 3.88 2.29 0.63
Flavanoids: 0.34 5.08 2.03 1.00
Nonflavanoid Phenols: 0.13 0.66 0.36 0.12
Proanthocyanins: 0.41 3.58 1.59 0.57
Colour Intensity: 1.3 13.0 5.1 2.3
Hue: 0.48 1.71 0.96 0.23
OD280/OD315 of diluted wines: 1.27 4.00 2.61 0.71
Proline: 278 1680 746 315
============================= ==== ===== ======= =====
:Missing Attribute Values: None
:Class Distribution: class_0 (59), class_1 (71), class_2 (48)
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
This is a copy of UCI ML Wine recognition datasets.
https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data
The data is the results of a chemical analysis of wines grown in the same
region in Italy by three different cultivators. There are thirteen different
measurements taken for different constituents found in the three types of
wine.
Original Owners:
Forina, M. et al, PARVUS -
An Extendible Package for Data Exploration, Classification and Correlation.
Institute of Pharmaceutical and Food Analysis and Technologies,
Via Brigata Salerno, 16147 Genoa, Italy.
Citation:
Lichman, M. (2013). UCI Machine Learning Repository
[https://archive.ics.uci.edu/ml]. Irvine, CA: University of California,
School of Information and Computer Science.
.. topic:: References
(1) S. Aeberhard, D. Coomans and O. de Vel,
Comparison of Classifiers in High Dimensional Settings,
Tech. Rep. no. 92-02, (1992), Dept. of Computer Science and Dept. of
Mathematics and Statistics, James Cook University of North Queensland.
(Also submitted to Technometrics).
The data was used with many others for comparing various
classifiers. The classes are separable, though only RDA
has achieved 100% correct classification.
(RDA : 100%, QDA 99.4%, LDA 98.9%, 1NN 96.1% (z-transformed data))
(All results using the leave-one-out technique)
(2) S. Aeberhard, D. Coomans and O. de Vel,
"THE CLASSIFICATION PERFORMANCE OF RDA"
Tech. Rep. no. 92-01, (1992), Dept. of Computer Science and Dept. of
Mathematics and Statistics, James Cook University of North Queensland.
(Also submitted to Journal of Chemometrics).
Diese Daten sind also eigentlich für die Klassifikation gedacht - es gibt drei bekannte Zielklassen (wines[“target]). Wir werden die Zielklassen zunächst ignorieren und nur mit den Featurewerten (Spalte “data”) explorativ clustern.
# Zur Information für später: Wie sind die Zielklassen verteilt?
print(wines["target"])
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
Um zu verhindern, dass die absoluten Größen verschiedener Features das Clustering verzerren, skalieren wir die Daten. Der StandardScaler führt eine sog. z-Transformation durch. Das bedeutet, dass die Daten zentriert werden (d.h., es wird nur die Abweichung vom Mittelwert betrachtet) und dass die Varianz jedes Features normiert wird. Die Skalierung ist wegen der Berechnung von Mittelwert und Standardabweichung immer für den zugrundeliegenden Datensatz korrekt - neue Daten mit deutlich größeren/kleineren Featurewerten als bisher können nicht angemessen skaliert werden.
Wegen der Berechnung von Mittelwert und Standardabweichung ist das Verfahren auch gegenüber Outliern (= sehr untypische Datenpunkte) empfindlich. Wenn Ihr Datensatz Outlier enthält, empfiehlt sich z.B. der RobustScaler.
# Daten skalieren
scaler = StandardScaler()
data_scaled = scaler.fit_transform(wines.data);
# K-Means anwenden. Wir wissen, dass 3 Zielklassen existieren, daher erwarten wir n_clusters=3 Cluster
# Bei Daten ohne Zielklasse muss dieser Parameter variiert werden!
# Wir geben an, mit welchem random_state die zufälligen Anfangszentroide festgelegt werden sollen.
kmeans = cluster.KMeans(n_clusters=3, random_state=0, n_init=10).fit(data_scaled)
# Welche Cluster wurden für die Instanzen gefunden?
print(kmeans.labels_)
[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 0 1 1 1 1 1 1 1 1 1 1 1 2
1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
Das sieht ja recht aufgeräumt aus - die Daten sind ja im Original nach Zielklassen sortiert, diese scheinen durchaus ansatzweise getroffen zu werden.
Aufgabe: Wie sieht die Vorhersage aus, wenn man die Daten nicht vorab skaliert?
Intuitiver Evaluationsansatz 1: Größe.#
# Wie groß sind die Cluster? Wir möchten 3 Cluster sehen.
for i in range(0,3):
print("Name:", i, "Größe: ", list(kmeans.labels_).count(i))
# Wir können uns auch die Zentroide anzeigen lassen - diese geben Aufschluss über die Charakteristika der Cluster
# und sind daher für die Interpretation der Cluster nützlich.
print (kmeans.cluster_centers_)
Name: 0 Größe: 51
Name: 1 Größe: 66
Name: 2 Größe: 61
[[ 0.16490746 0.87154706 0.18689833 0.52436746 -0.07547277 -0.97933029
-1.21524764 0.72606354 -0.77970639 0.94153874 -1.16478865 -1.29241163
-0.40708796]
[-0.93900326 -0.39196582 -0.43920097 0.20898793 -0.46377382 -0.05334831
0.06690377 -0.01982215 0.06479192 -0.88207529 0.45298189 0.28973833
-0.75602559]
[ 0.87809728 -0.30457633 0.31894179 -0.66452366 0.56488825 0.87650546
0.94363903 -0.58558981 0.58178294 0.16718842 0.48372814 0.76705349
1.15834713]]
Die Clusterverteilung ist relativ gleichmäßig, was positiv ist: Sie bekommen sonst oft ein riesiges “Restcluster” und einige kleinere Cluster. Die Clustergröße passt grob, aber nicht perfekt zu den bekannten Zielklassen.
Wenn Sie die Featurewerte der Zentroide (also die Durchschnittswerte über alle Instanzen der Cluster) ansehen, sehen Sie deutlich die unterschiedlichen Charakteristika der Cluster. Z.B. ist Feature 1 in Cluster 2 maximal und in Cluster 1 minimal.
Aufgabe: Experimentieren Sie mit unterschiedlichen random_states. Bekommen Sie andere Verteilungen?
2.6. Numerische Evaluation#
Die intuitive Evaluation hat uns einen Eindruck von den Clustern verschafft, ist aber mühsam und ungenau. Insbesondere, wenn wir verschiedenen Algorithmen oder Parameter vergleichen wollen, wäre es schön, Zahlen erheben und vergleichen zu können.
Hierzu gibt es zwei Strategien: Wenn Zielklassenannotation vorliegt, kann man die Cluster-Zuweisungen mit den annotierten Zielklassen vergleichen (überwachte Evaluation). Damit kann man z.B. sehen, ob die Zielklassen in sich konsistent und anhand der Featurekombinationen klar unterscheidbar sind.
Wenn keine Zielklassen vorliegen, kann man die Form der gebildeten Cluster verwenden: Sie sollen möglichst kompakt und klar gegen einander abgegrenzt sein.
Evaluation mit Zielklassen#
Glücklicherweise sind die Wein-Daten annotiert, sodass wir die Ergebnisse überwacht auswerten können. Wir verwenden die Maße Homogenität, Vollständigkeit und V-Maß (weitere Maße finden Sie im User Guide von SciKit-Learn ).
Die Homogenität einer Clustermenge gibt an, wie sauber die Cluster die Zielklassen trennen. Wenn sich in jedem Cluster nur Elemente derselben Zielklasse befinden, ist die Homogenität 1. Dies ist natürlich der Fall, wenn die Cluster die Zielklassen genau abbilden – aber es gilt übrigens auch, wenn es z.B. für jede Zielklasse mehrere Cluster gibt. Es wird nur betrachtet, ob die Cluster Zielklassen vermischen.
Die Vollständigkeit gibt im Gegenteil an, zu welchem Prozentsatz alle Elemente einer Zielklasse auch im selben Cluster gefunden werden. Hier erreicht man natürlich auch den Wert 1, wenn die Cluster die Zielklassen perfekt abbilden - aber auch dann, wenn es nur ein einziges Cluster mit allen Datenpunkten gibt (hier wäre die Homogenität natürlich 0). Umgekehrt gäben zwei homogene Cluster pro Zielklasse geringe Vollständigkeit.
Da Homogenität und Vollständigkeit zwei verschiedene Aspekte der Cluster-Zuordnung betrachten und beide hoch sein sollten, werden sie im V-Maß zusammengefasst, das ihren geometrischen Mittelwert berechnet. Die Formel lautet also v=(homogeneity x completeness) / (homogeneity + completeness)
hom = metrics.homogeneity_score(wines["target"],kmeans.labels_)
com = metrics.completeness_score(wines["target"],kmeans.labels_)
vmeasure = metrics.v_measure_score(wines["target"],kmeans.labels_)
print(hom)
print(com)
print(vmeasure)
0.8954455657307514
0.8897429811300377
0.8925851652969188
Bei den Wein-Daten ist die Passung von Cluster-Ergebnis und annotierten Zielklassen ziemlich gut (das hatte man ja schon bei der Auflistung der Klassenvorhersage gesehen).
Dies ist ein gutes Zeichen für die spätere Klassifikation: Die annotierten Zielklassen ergeben sich ziemlich eindeutig aus den Features.
Evaluation ohne Zielklassen#
Wenn (wie meistens) keine Zielklassen-Annotation existiert, kann eine beste Cluster-Aufteilung aufgrund der Form ihrer Cluster ausgewählt werden. Hierbei ist die Intuition, dass Clusterelemente dicht beieinander liegen und Cluster klar von einander getrennt sein sollten.
In erster Näherung sieht man dies an der inertia (Trägheit) der Cluster; das ist die Summe des quadrierten (damit die Richtung herausfällt) Abstands jedes Datenpunkts zu seinem Cluster-Zentroiden. Je geringer die inertia, desto kompakter die Cluster. Dieses Maß wird vom K-Means-Algorithmus bei der Ausführung minimiert, kann aber auch für andere Cluster-Algorithmen berechnet werden.
Etwas komplexer ist der Silhoutte Coefficient zu berechnen. Hier berechnet man sowohl den durchschnittlichen Abstand jedes Datenpunkts zu seinen Clustergenossen, als auch den durchschnittlichen Abstand zu den Mitgliedern des nächstgelegenen anderen Clusters. Ist der erstgenannte durchschnittliche Abstand klein, sind die Cluster kompakt. Ist der letztgenannte durchschnittliche Abstand groß, liegen sie weit auseinander und es gibt wenig “Grenzgänger”, die praktisch genau zwischen zwei Clustern liegen. In diesem Fall ergibt sich ein hoher Silhouette Coefficient. Je höher also der Wert, desto besser die Cluster.
inertia = kmeans.inertia_
sil = metrics.silhouette_score(data_scaled,kmeans.labels_)
print(inertia)
print(sil)
1278.7607763668145
0.28594199657074876
Diese Evaluationswerte sagen uns als Einzelwerte noch nicht viel. Sie werden erst durch den Vergleich interessant, zum Beispiel, wenn wir verschiedene random_states ausprobieren. Um das effizient und gut wartbar zu tun, definieren wir uns eine Evaluationsfunktion, die unser trainiertes Modell mit Hilfe der verschiedenen Evaluationsmethoden bewertet und die Ergebnisse ausgibt.
Der Code ist adaptiert von einem sklearn-Codebeispiel.
def bench_k_means(kmeans, name, data, labels):
"""Benchmark to evaluate the KMeans initialization methods.
Parameters
----------
kmeans : KMeans instance
A :class:`~sklearn.cluster.KMeans` instance that has already been trained
name : str
Name given to the strategy. It will be used to show the results in a
table.
data : ndarray of shape (n_samples, n_features)
The data whose clusters should be evaluated.
labels : ndarray of shape (n_samples,)
The labels used to compute the supervised clustering metrics.
"""
# Inertia
results = [name, kmeans.inertia_]
# The silhouette score requires the full dataset
results += [
metrics.silhouette_score(data_scaled, kmeans.labels_,
metric="euclidean")
]
# Supervised metrics which require the true labels and cluster
# labels
clustering_metrics = [
metrics.homogeneity_score,
metrics.completeness_score,
metrics.v_measure_score,
]
results += [m(labels, kmeans.labels_) for m in clustering_metrics]
# Show the results
formatter_result = ("{:9s}\t{:.0f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}")
print(formatter_result.format(*results))
# Aufrufen der Benchmark mit unserem trainierten kmeans und einer zufälligen Zuweisung (zum Vergleich)
# Fügen Sie hier auch Ihren günstigeren random_state von oben ein!
print(82 * '_')
print('init\t\tinertia\tsil\thom\tcom\tv-meas')
# unser kmeans-Modell (zur Sicherheit neu trainieren)
kmeans = cluster.KMeans(n_clusters=3, n_init=10, random_state=0).fit(data_scaled)
bench_k_means(kmeans=kmeans, name="k-means", data=data_scaled, labels=wines["target"])
# zufällige Cluster-Zuordnung erzeugen
kmeans_rand = cluster.KMeans(init="random", n_clusters=3, n_init=10, random_state=0).fit(data_scaled)
bench_k_means(kmeans=kmeans_rand, name="random", data=data_scaled, labels=wines["target"])
print(82 * '_')
__________________________________________________________________________________
init inertia sil hom com v-meas
k-means 1279 0.286 0.895 0.890 0.893
random 1278 0.285 0.879 0.873 0.876
__________________________________________________________________________________
Jetzt können wir auch fundierter ausprobieren, was beim Variieren des random state passiert. Entweder, wir generieren von Hand neue kmeans-Modelle, oder wir setzten die Variable n_init; sie gibt an, wie oft das Modell mit neuen Zufallsstartwerten trainiert werden soll. Es gewinnt dann das Modell mit der geringsten inertia.
# Aufrufen der Benchmark mit unserem trainierten kmeans und einer zufälligen Zuweisung (zum Vergleich)
# Fügen Sie hier auch Ihren günstigeren random_state von oben ein!
print(82 * '_')
print('init\t\tinertia\tsil\thom\tcom\tv-meas')
# unser kmeans-Modell (zur Sicherheit neu trainieren)
kmeans = cluster.KMeans(n_clusters=3, n_init=10, random_state=0).fit(data_scaled)
bench_k_means(kmeans=kmeans, name="k-means_0", data=data_scaled, labels=wines["target"])
# unser kmeans-Modell (random_state 42)
kmeans = cluster.KMeans(n_clusters=3, n_init=10, random_state=42).fit(data_scaled)
bench_k_means(kmeans=kmeans, name="k-means_42", data=data_scaled, labels=wines["target"])
# unser kmeans-Modell (10x trainiert; das Modell mit der besten inertia gewinnt)
kmeans = cluster.KMeans(n_clusters=3, n_init=10).fit(data_scaled)
bench_k_means(kmeans=kmeans, name="k-means_opti", data=data_scaled, labels=wines["target"])
# zufällige Cluster-Zuordnung erzeugen
kmeans_rand = cluster.KMeans(init="random", n_init=10, n_clusters=3, random_state=0).fit(data_scaled)
bench_k_means(kmeans=kmeans_rand, name="random", data=data_scaled, labels=wines["target"])
print(82 * '_')
__________________________________________________________________________________
init inertia sil hom com v-meas
k-means_0 1279 0.286 0.895 0.890 0.893
k-means_42 1278 0.285 0.879 0.873 0.876
k-means_opti 1278 0.285 0.879 0.873 0.876
random 1278 0.285 0.879 0.873 0.876
__________________________________________________________________________________
Das Ergebnis zeigt, dass unser K-Means mit random_state 0 (unser erstes Modell) im Sinne der inertia minimal etwas besser clustert als die anderen. Die überwachte Evaluation von Homogenität, Vollständigkeit und entsprechend auch V-Maß zeigt dasselbe Bild.
Im Vergleich mit k-means_0 wird auch das optimierte Modell mit 10 Testläufen nicht besser. Offenbar war keiner der zufälligen Startwerte besser als der, der zum random_state=0 gehört.
Das relativ eintönige Bild bei den späteren K-Means-Varianten stammt wahrscheinlich von der kleinen Anzahl Cluster und kann für Ihre Daten deutlich anders aussehen. Ebenso muss die Bewertung aufgrund von unüberwachten Evaluationsmaßen nicht der Bewertung durch überwachte Maße entsprechen.
Parameter setzen mit Hilfe von Evaluationsmaßen#
In unserem Beispiel ist die Anzahl der Cluster vorgegeben, weil wir Daten mit bekannten Zielklassen verwenden. Die Anzahl der zu findenden Cluster ist für viele Algorithmen ein wichtiger Parameter. Sie können ihn setzen, indem Sie die Clusterzahl variieren und jedes Ergebnis evaluieren. Die Anzahl Cluster, die am besten evaluiert wird, wird gewählt.
Sie finden bei Bedarf ein Beispiel unter scripts/modeling-clustering-parameters.ipynb für das Parametersetzen für einen weiteren Datensatz und zwei Algorithmen. Im Beispiel zeigt sich deutlicher, dass nicht jedes Evaluationsmaß gleichermaßen informativ ist, wenn es um die Auswahl einer für den Menschen sinnvollen Cluster-Konfiguration geht.
2.7. Weitere Aufgabenstellungen#
Unser Beispiel funktioniert auf einem klassischen Datensatz mit rein numerischen Features. Schwieriger wird es, wenn Sie z.B. Textdaten clustern wollen - hier müssen Sie zunächst eine Repräsentation finden, die der K-Means-Algorithmus nutzen kann.
Man verwendet in diesem Fall üblicherweise einen Vektorisierungsfilter (z.B. den TfIdfVectorizer), der die häufigsten Wörter im Text bestimmt, als Dimensionen interpretiert, und die Dimensionen für jeden Text mit der Auftretenshäufigkeit des Worts befüllt. Dies funktioniert auch für einzelne Textfeatures!
Ein Beispiel finden Sie bei Scikit Learn
2.8. Weitere Algorithmen#
Sie finden unter https://scikit-learn.org/stable/modules/clustering.html# eine Übersicht über weitere Clustering-Algorithmen, die in scikit-learn implementiert sind. Im Abschnitt 2.3.1 sehen Sie, wie diese Algorithmen mit verschieden verteilten (synthetischen) Datensätzen zurecht kommen. Wählen Sie je nach Interesse einen Algorithmus aus und lesen Sie sich ein.
Bearbeiten Sie dann mit Ihrem ausgewählten Algorithmus die Gesichter-Clustering-Aufgabe, die bisher mit K-Means gelöst ist. Wir vergleichen in der Präsenz Ihre Beobachtungen mit verschiedenen Algorithmen. Variieren Sie daher auch die Parameter Ihres Ansatzes bei der Evaluation.