Klassifikation

3. Klassifikation#

Bei einer Klassifikationsaufgabe wollen wir Datenpunkten Klassen zuweisen, die im Vorhinein definiert wurden. Wir können z.B. Email in Spam und Ham sortieren, Restaurantbewertungen die entsprechenden Sterne zuordnen oder Tickets dem richtigen Bearbeiter zuleiten.

Zum Teil könnte man diese Aufgaben auch lösen, wenn man ohne Betrachtung realer Daten feste Regeln erstellen würde. Effizienter ist aber, Lernalgorithmen die Aufgabe zu stellen, selber aus den Daten die entsprechenden Regelmäßigkeiten zu lernen. Dafür brauchen sie Beispiele, also eine möglichst große Menge an Trainingsdaten, die mit den gewünschten Zielklassen annotiert sind. Mathematisch gesehen lernen sie dann eine Funktion aus den Features der Datenpunkte in die Zielklassen.

Wie genau diese Funktion aussieht und wie sie gelernt wird hängt vom gewählten Algorithmus ab. Die Auswahl hängt von mehreren Kriterien ab:

Die gegebenen Daten. Einige Algorithmen haben spezielle Anforderungen an die Datentypen der Features oder brauchen erfahrungsgemäß viele Trainingsdaten (Faustregel: Je mehr Parameter der Algorithmus lernt, desto mehr Evidenz braucht er; neuronale Netze z.B. lernen sehr viele Gewichtsparameter und sind daher sehr datenhungrig). Welche Anforderungen ein Algorithmus in diese Richtung hat, können Sie gut bei Witten, Frank & Hall (s. HFT-Bibliothek) nachlesen. Die sklearn-Dokumentation eignet sich nur eingeschränkt.
Die Anforderungen an die Interpretierbarkeit des Algorithmus. Brauchen Sie nur die Zielklassen, um eine andere Aufgabe zu lösen? Oder sind Sie im Bereich der Datenexploration und Modellentwicklung und möchten die Ergebnisse besser verstehen und die Daten tiefer interpretieren? Algorithmen wie Entscheidungsbäume oder logistische Regression erstellen quasi Wichtigkeitsbewertungen für die Features und können helfen, das Lernerergebnis zu erklären. Mehr zum Thema Evaluation und Erklärbarkeit im entsprechenden Abschnitt gegen Ende des Kurses!
Die aktuelle Mode. Wir erleben typischerweise alle 5-10 Jahre eine neue “Mode”: Ein neuer Algorithmus wird aus einem verwandten Fach auf eine für uns relevante Aufgabe übertragen, sieht vielversprechend aus und wird in der Folge im Sinne von “if you have a hammer” flächendeckend eingesetzt. Irgendwann ergibt sich ein Verständnis, in welchen Szenarien sich der Algorithmus gut einsetzen lässt und in welchen schlechter. Die Innovation ergibt sich oft daraus, das leistungsfähige Algorithmen durch einen weiteren Preissturz bei Speicherplatz und Rechenkapazität für interessant große Probleme überhaupt erst anwendbar werden. Aktuell sind Neuronale Netze (Deep Learning) die prestigeträchtigste Methode. Ihre Leistungsfähigkeit ist groß, aber aufgrund des großen Datenbedarfs sollte man sie nicht blind einsetzen.

Unabhängig vom gewählten Algorithmus sind Klassifikationsaufgaben unterschiedlich schwer. Je informativer die Features mit Bezug auf die Zielklasse sind und je weniger Zielklassen unterschieden werden müssen, desto einfacher das Problem. Wenn die Features nur wenig Information über die Zielklasse liefern, einzelne Zielklassen sehr selten sind (und daher wenig Evidenz haben) oder viele sehr ähnliche Zielklassen existieren, ist die Aufgabe sehr schwierig.

Das gilt übrigens auch für den Menschen - die Annotation der Klassen an die Trainingsdaten geschieht ja von Hand, und auch Menschen finden es komplizierter, 10 Zielklassen zu unterscheiden als zwei, insbesondere, wenn drei der Zielklassen so gut wie nie vorkommen und schwer zu unterscheiden sind. Entsprechend gibt es in solchen Fällen oft auch Qualitätsmängel an der Annotation, die eine gute Zuordnung durch den Lernalgorithmus weiter erschweren. Wenn Sie Einfluss auf die Annotation haben, achten Sie darauf, dass es wenige, klar umrissene Klassen gibt und sich die Annotatoren besonders am Anfang immer wieder über die Annotation austauschen und unklare Fälle entscheiden.

Wenn Sie schließlich gute Daten erhoben und einen Algorithmus ausgewählt haben, wartet noch der saubere Umgang mit Test- und Trainingsdaten als Stolperstein. Sie haben in Kap. 3.4 schon unter “Typische Fehler” davon gehört…

Aufgabe: Warum ist die Trennung in Trainings- und Testdaten (oder Trainings-, Entwicklungs- und Testdaten) so wichtig?

Das grundsätzliche Vorgehen ist Folgendes:

geeignetes Lernverfahren wählen
Daten aufbereiten
Daten aufteilen
geeignete Features berechnen und auswählen
Parameter des Algorithmus setzen (3+4 bedingen sich potentiell gegenseitig!)
Klassifikation von ungesehenen Testdaten
Evaluation und Interpretation anhand der Testdaten

Es folgt jetzt zuerst Hintergrundinformation zu den Punkten 0, 2 und 6.

Zu 1 führen wir beispielhaft einen mächtigen und etablierten Klassifikationsalgorithmus ein: Die Support Vector Machine (Hype-Algorithmus der frühen 2000er). Weitere Algorithmen recherchieren Sie nach Bedarf im oben genannten Witten, Frank & Hall oder im sklearn User Guide.

Zu 3 erkläre ich die datensparsame Methode der Crossvalidation (Kreuzvalidierung).

Ein letzter Schwerpunkt liegt bei Punkt 7 und den angemessenen Evalutionsmaßen, die wir aus der Konfusionsmatrix ableiten. Die Matrix und die Maße interpretieren zu können, ist ein erster wichtiger Schritt beim Verstehen der Ergebnisse.

Wie immer können Sie Punkte, die Sie schon kennen, überfliegen. Sie können für die Praxisaufgabe auch die reinen Codezellen verwenden.

Zum Abschluss arbeiten wir alle Schritte an einem Beispiel durch - natürlich mit der SVM. Zusätzlich zum Vorgehen bei der Klassifikation führen wir darin sklearn-Pipelines ein. Sie ermöglichen es, die Datenaufbereitung und das Algorithmentraining übersichtlich und gekapselt darzustellen und in der Kombination mit Grid Search die Parameter mehrerer Verarbeitungsschritte sauber gemeinsam zu optimieren (z.B. 3 und 4).

3.1. Algorithmus: Support Vector Machine#

Die Support Vector Machine arbeitet mit einer einfachen Intuition: Wenn wir unseren Datensatz vor uns haben, möchten wir wie in Abb. 1 eine Linie zwischen den Datenpunkten ziehen, die die Entscheidungsgrenze darstellt. Auf jeder Seite der Linie finden sich dann nur noch Datenpunkte einer Klasse.

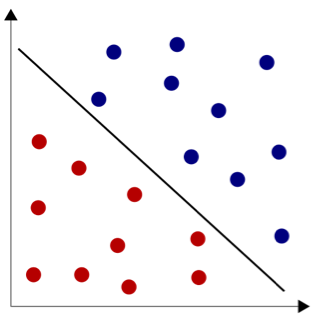linearSeparabel Abb. 1: Linear separable Klassifikationsaufgabe, Mekeor - Eigenes Werk, CC BY-SA 3.0

Wenn Sie die Abbildung genau betrachten, stellen Sie fest, dass es noch viel mehr mögliche Entscheidungslinien gibt, die zwischen den Instanzen der beiden Klassen verlaufen und sie sauber trennen: Sie könnte etwas steiler, etwas flacher oder überhaupt überall auf der freien Fläche zwischen den Datenpunkten liegen! Wo die Entscheidungsgrenze genau verläuft, ist aber nicht egal: Sobald ein ungesehener Datenpunkt klassifiziert werden soll, kann ihre genau Position den Zuschlag zur einen oder der anderen Klasse geben.

Wir möchten, dass die Entscheidungsgrenze so weit wie möglich aus den Daten abgeleitet wird. Deshalb suchen wir wie in Abb. 2 zunächst zwei parallele Gerade, die auf den Datenpunkten an der Klassengrenze aufliegen, um den möglichen Bereich für die Entscheidungsgrenze zu definieren. Die Datenpunkte, durch die die Geraden führen, heißen Stützvektoren (support vectors - in der Abb. rot). Für einen höherdimensionalen Datensatz sind die Gerade Ebenen und die Benennung ergibt mehr Sinn.

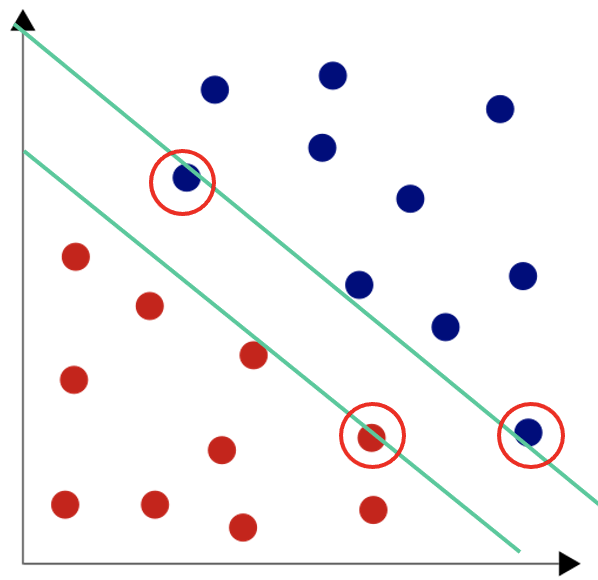Abb. 2: Stützvektoren definieren den Verlauf des Entscheidungskorridors.

Den entstehenden Entscheidungskorridor teilen wir jetzt genau auf der Hälfte; hier ist der “gerechteste” Verlauf der Entscheidungsgrenze. Wir haben jetzt durch die Stützvektoren den Korridor bestmöglich aus den Daten abgeleitet und den finalen Verlauf der Entscheidungsgrenze so festgelegt, dass keine Klasse einen Vorteil hat. Das Inferieren des Entscheidungskorridors ist ein Optimierungsproblem, das z.B. mit Quadratic Programming gelöst wird.

Wir haben jetzt eine schöne Lösung für Klassifikationsprobleme, die sich mit einer linearen Entscheidungsgrenze lösen lassen (sog. linear separable Probleme). Im Prinzip lässt sich die Entscheidungsgrenze für die Klassifikation natürlich auch als Funktion für die Regression fassen.

Leider sieht die Realität oft anders aus und die Entscheidungsgrenze verläuft eher wie in Abb. 3: 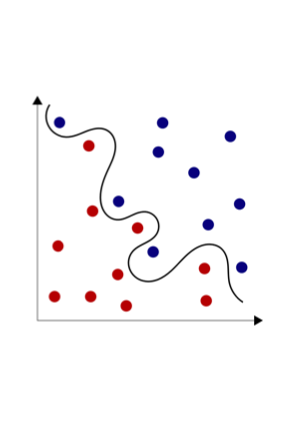nichtLinearSeparabel Abb. 3: Nicht linear separable Klassifikationsaufgabe, Mekeor - Eigenes Werk, CC BY-SA 3.0

Hier hilft ein weiterer Trick (quasi direkt aus Star Trek): Der Sprung in eine höhere Dimension. Abb. 4 zeigt ein Beispiel für ein Problem, das in seiner Original-Dimensionalität nicht linear separabel ist, aber in einer höheren Dimension linear separabel wird: In nur einer Dimension gibt es keine lineare Entscheidungsgrenze zwischen roten und blauen Instanzen; kommt die zweite Dimension hinzu, können sich die Datenpunkte ihr entlang auffächern und das Problem wird linear separabel.

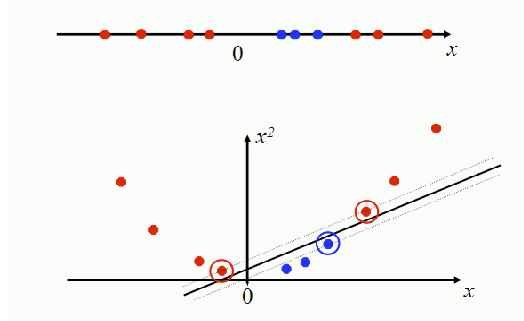Dimensionssprung Abb. 4: Lineare Separabilität in einer höheren Dimension. Aus: Introduction to Information Retrieval, Manning, Raghavan & Schütze (2008)

Um nicht linear separable Problem lösen zu können, müssen wir also “nur” unsere Daten in einen höherdimensionalen Raum transformieren, die Entscheidungsgrenze dort berechnen und auf unsere hochtransformierten Testdaten anwenden. Dies ist rechenaufwendig; daher verwendet man sog. Kernel. Sie beschreiben quasi die Entfernung von Datenpunken im hochdimensionalen Raum und helfen so bei der Berechnung der Entscheidungsgrenze, ohne transformieren zu müssen. (Wenn Sie möchten, lesen Sie die Details in Introduction to Information Retrieval, Manning, Raghavan & Schütze (2008))

Kernel gibt es in vielen Varianten. Sie haben neben ihrer Eigenschaft der Abstandsbeschreibung auch eine intuitive Interpretation: Ein polynomieller Kernel erlaubt es uns, Features zu kombinieren (und zwar so viele, wie der Grad des Polynoms vorgibt). Das ist sehr nützlich, wenn erst eine Kombination von Features die Zielklasse vorhersagt (“wenn ‘nicht flugfähig’ und Umgebungstemperatur=’kalt’: Pinguin”). Eine radial basis function (rbf) erlaubt kreisförmige (bzw. kugelförmige) Entscheidungsgrenzen. Für Textklassifikation gibt es spezielle String-Kernels, die String-Ähnlichkeit geeignet definieren.

3.2. Datenaufteilung: Kreuzvalidierung#

Unser Ziel ist, generalisierbare Aussagen aus unseren Ergebnisse ableiten zu können. Dafür brauchen wir ungesehene Testdaten. Während der Modellerstellung gibt es immer wieder Parameter zu setzen oder die Entscheidung zwischen verschiedenen Verfahren zu treffen. Natürlich möchten wir so entscheiden, dass die optimale Performanz entsteht - wir dürfen aber die Testdaten nicht zum Ausprobieren verwenden! Sonst würden wir ja diejenige Entscheidung treffen, die für die Testdaten optimal funktioniert, und damit sind sie nicht mehr ungesehen.

Wir müssen also die Trainingsdaten aufteilen, um einen Datensatz zum Parametersetzen zu haben. Dieser Datensatz heißt Entwicklungsdaten (development data). Allerdings bedeutet diese Aufteilung, dass die Trainingsdaten kleiner werden. Gerade, wenn wenig annotierte Daten zur Verfügung stehen, kann das problematisch sein.

Als Alternative zur festen Aufteilung gibt es die Kreuzvalidierung: Wir teilen die Trainingsdaten in k Teile (z.B. drei, fünf oder 10). Nun wird jeder Datenabschnitt ein Mal zu den Testdaten, während wir auf den übrigen Daten trainieren. Wikipedia bietet eine schöne Visualisierung für eine 3-fache Kreuzvalidierung: Wir trainieren drei verschiedene Modelle jeweils auf den Trainingsdaten (zwei der drei Datenabschnitte) und testen auf dem verbleibenden Testabschnitt. Insgesamt haben wir also für jeden Datenpunkt eine Testvorhersage gemacht, die Vorhersagen waren aber alle von Modellen, die nicht auf den Datenpunkten trainiert waren.

Die Kreuzvalidierung ist also nützlich, wenn eine begrenzte Menge Trainingsdaten für das Parametersetzen zur Verfügung steht. Wenn alle Parameter feststehen, nutzt man für das Trainieren des finalen Modells die gesamten Trainingsdaten und evaluiert ein letztes Mal auf den ungesehenen Testdaten.

3.3. Evaluation: Konfusionsmatrix und Precision/Recall/F-Score#

Die Evaluation soll uns sagen, wie gut das Modell vorhergesagt hat. Ein erstes, einfaches Maß ist die Accuracy: Sie zählt, wie viel Prozent der Testdaten korrekt vorhergesagt wurden.

Für weitere Verbesserungen des Modells im Modellierungskreislauf ist aber auch interessant, welche Fehler das Modell gemacht hat. War eine Klasse besonders schwer oder einfach vorherzusagen? Gibt es Klassen, die oft mit einander verwechselt werden? Um das besser einschätzen zu können, tragen wir die Vorhersagen und die annotierten Zielklassen (gold labels) in einer Matrix auf (Tab. 1). Im Beispiel soll der Datensatz 100 Datenpunkte enthalten.

Tab. 1: Konfusionsmatrix für einen Beispieldatensatz
	wirklich A	wirklich B	Zeilensumme
Vorhersage A	50	10	Σ60
Vorhersage B	5	35	Σ40
Spaltensumme	Σ 55	Σ 45

`

Diese Matrix zeigt, dass mit den Vorhersagen grundsätzlich alles in Ordnung ist - die Vorhersagen und die Goldlabel stimmen im Großen und Ganzen überein (s. Diagonalzellen “Vorhersage A”/”wirklich A” und “Vorhersage B”/”wirklich B”). Die Accuracy ist die Summe der korrekten Vorhersagen durch alle Vorhersagen: \( \frac{50 + 35}{(50+10+5+35)}\) = 85%.

In den Zeilen der Matrix bekommt man einen Eindruck von der Verlässlichkeit der Vorhersagen: Wenn Klasse A vorhergesagt wird, ist das in 83% der Fälle richtig (50 aus 60 Vorhersagen insgesamt); für die Klasse B sind es 88% (35 aus 40). Dieses Maß nennt man die Precision. Sie wird klassenweise berechnet: korrekte Vorhersagen für die Klasse/alle Vorhersagen für die Klasse.

Bis hierher sieht also alles gut aus. Aber wenn man die Matrix spaltenweise betrachtet, gibt es doch ein Problem: Von 45 Datenpunkten, die zur Klasse B gehören, wurden nur 35 (78%) korrekt erkannt! Dieses Bild ist typisch für ungleich verteilte Klassen. Der Lerner sagt die häufigere Klasse auch häufiger voraus, und macht damit bei der selteneren Klasse Fehler. Diese fallen ziemlich ins Gewicht, weil eben von vornherein nicht so viele relevante Instanzen da waren. Wäre Klasse B für uns besonders interessant, würden uns 22% der relevanten Datenpunkte verloren gehen.

Diese Betrachtung quantifiziert man (wieder für jede Klasse einzeln) im Recall: Hierfür teilt man die korrekt als B erkannten Datenpunkte durch alle Datenpunkte, die tatsächlich zu B gehören.

In unserem Fall hat die Klasse A also eine Precision von 83% (50/(50+10)) und einen Recall von 91% (50 /(50+5)).

Die Klasse B hat eine Precision von 88% (35/(5+35)) und einen Recall von 78% (35/(10+35)).

Diese Zahlen zeigen recht deutlich, was das Problem mit dem aktuellen Modell ist: Der Lerner sagt häufig Klasse A voraus und erzeugt so einen sehr guten Recall für A. Im Umkehrschluss ist aber der Recall von B schlecht, es fallen relevante Instanzen unter den Tisch. Entsprechend ist die Vorhersage “A” nicht ganz so zuverlässig wie die Vorhersage “B” (die ja seltener gemacht wird und dann auch eher stimmt). Wenn uns Klasse B interessiert, würden wir jetzt versuchen, ihren Recall zu verbessern, möglichst ohne dass die Precision sinkt. (Das ist allerdings sehr schwierig - Precision und Recall sind selten balanciert).

Bislang haben wir Precision und Recall für einzelne Klassen betrachtet. Um zu einem Wert für den gesamten Klassifikator zu kommen, berechnen wir den gewichteten Mittelwert über alle Klassen. Damit gehen Klassen mit mehr Instanzen (bezogen auf die Testdaten, die der Evaluation zugrunde liegen) stärker ein als Klassen mit wenig Instanzen.

Der F-Score fasst die beiden Sichten auf die Klassifikation, nämlich Precision und Recall, in einer Zahl zusammen: F=2PR/(P+R). Damit werden verschiedene Klassifikatoren mit Hilfe eines einzelenen Wertes vergleichbar, auch wenn wir Detailinformation verlieren.

Man kann aus der Konfusionsmatrix auch noch andere klassenabhängige Evaluationsmaße ableiten. Dazu benennt man die Zellen der Matrix wie in Tab. 2, und zwar aus Sicht der jeweiligen Klasse: True Positive (korrekt vorhergesagt), True Negative (korrekt als nicht zur Klasse gehörig vorhergesagt), False Positive (inkorrekt als zur Klasse gehörig vorhergesagt - Instanz fälschlich eingemeindet) und False Negative (inkorrekt als nicht zur Klasse gehört vorhergesagt - Instanz übersehen).

Tab. 1: Konfusionsmatrix mit Zellbezeichnungen aus Sicht der Klasse B
	wirklich A	wirklich B
Vorhersage A	True Negative	False Negative
Vorhersage B	False Positive	True Positive

`

Aufgabe: Die Wikipedia-Seite zur Konfusionsmatrix verwendet als Beispiel einen Test für eine Krankheit (übrigens schon seit vor 2020…). Entsprechen die dort vorgestellten Maße “Sensitivität” und “Spezifität” Maßen, die hier eingeführt wurden? Wenn ja, welchen?

3.4. Praxisbeispiel: Texte klassifizieren#

# Imports für unten

from sklearn.datasets import fetch_20newsgroups

from sklearn.model_selection import train_test_split

from sklearn.feature_extraction.text import TfidfVectorizer

from sklearn.feature_selection import SelectFromModel
from sklearn.svm import LinearSVC

from sklearn.pipeline import Pipeline

from sklearn.svm import SVC

from sklearn.model_selection import GridSearchCV

from sklearn.metrics import classification_report, confusion_matrix
from sklearn.model_selection import cross_val_predict

Schritt 1+2: Daten#

Wir benutzen einen Teil des “20 Newsgroups”-Korpus. Es handelt sich um Diskussionsforen zu einem bestimmten Thema, eine Art prähistorisches Reddit. Es gibt insgesamt knapp 19k Datenpunkte, dabei sind aber nicht alle Gruppen gleich stark vertreten. Die Daten wurden Mitte der 90er Jahre gesammelt und werden seitdem als Beispieldatensatz für die Textklassifizierung genutzt.

Die Aufgabe ist, die Posts ihren Newsgroups zuzuordnen.

Wir betrachten vier gut gegen einander abgrenzbare Gruppen: alt.atheism, talk.religion.misc, comp.graphics und sci.space. Der Use Case ist inspiriert von einem sklearn-Beispiel.

# Schritt 1: Daten aufbereiten
# -- wir verwenden ein Standardcorpus und wählen einen Teil davon aus.
# Wir möchten die Daten zusätzlich um Text bereinigen, der nicht zur Diskussion gehört (wie headers und footers)
# oder der schon anderweitig belegt ist (quotes aus vorherigen Nachrichten).

categories = [
        'alt.atheism',
        'talk.religion.misc',
        'comp.graphics',
        'sci.space',
    ]

remove = ('headers', 'footers', 'quotes')

# Schritt 2: Daten in Training und Test teilen
# -- das Korpus ist schon entsprechend unterteilt; wir laden train und test getrennt herunter.

data_train = fetch_20newsgroups(subset='train', categories=categories,
                                shuffle=True, random_state=42,
                                remove=remove)

data_test = fetch_20newsgroups(subset='test', categories=categories,
                               shuffle=True, random_state=42,
                               remove=remove)

# Wenn die Daten noch (weiter) aufgeteilt werden müssen, geht das am besten mit der 
# Methode sklearn.model_selection.train_test_split
# Sie liefert Features und Zielklassen für test und train zurück und lässt sich umfassend parametrisieren.

# Wir können also noch Entwicklungsdaten erzeugen, die 20% der Trainingsdaten umfassen und alle vier Zielklassen 
# gleichermaßen berücksichtigen (stratifizieren):

X_train, X_dev, y_train, y_dev = train_test_split(data_train['data'], data_train['target'], 
                                                    test_size=0.2, 
                                                    random_state=42,
                                                    stratify=data_train['target'])

Schritt 3a: Geeignete Features berechnen#

Die einfachste Repräsentation für jeden Post wäre die Liste der enthaltenen Wörter, zum Beispiel als Vektor mit den Wörtern als Dimensionen und der Vorkommenshäufigkeit für jedes Wort als Wert. Allerdings ergibt dies riesige, sehr spärlich besetzte Featurevektoren, weil jedes Wort in allen Posts repräsentiert werden muss. Außerdem generieren wir bedeutungslose Ähnlichkeit in den Dimensionen “and”, “but”, “we” usw., die häufig sind und in vielen Texten vorkommen.

Die modernste Art, mit dem Problem umzugegehen, sind sog. Embeddings, die von neuronalen Netzen gelernt werden.

Wir kommen aber auch ganz gut mit Methoden zurecht, die die Wörter für die Featurevektoren nach ihrer Wichtigkeit für das Dokument auswählen. Hier verwendet man standardmäßig den TF-IDF-Wert (term frequency - inverse document frequency). Er ist hoch für Wörter, die im aktuellen Dokument (hier: Newsgroup-Beitrag) häufig sind (TF ist die Anzahl an Vorkommen im Dokument), in anderen Dokumenten aber eher selten (DF ist die Anzahl an Dokumenten im gesamten Datensatz, in denen das Wort vorkommt). Damit werden Strukturwörter wie “and”, “but”, usw. effektiv ausgefiltert.

Zusätzlich kann man in einem Vorverarbeitungsschritt noch Stoppwörter ausfiltern; dies geschieht aufgrund einer Liste von typischen Strukturwörtern und bedeutet weniger TF-IDF-Berechnungen für den Datensatz. Bei der Verwendung von Stoppwortlisten ist aber Vorsicht geboten; je nach Themengebiet der Daten können vermeintliche Stoppwörter relevant sein. Z.B. wird manchmal “not” gefiltert; das Wort ist aber natürlich hoch relevant, wenn man versucht, die Bedeutung oder die positive/negative Stimmung eines Textes zu erkennen.

Der TfidfVectorizer von sklearn hat mehrere Parameter, darunter max_df und min_df. Hier kann man Wörter ausschließen, die im gesamten Datensatz extrem häufig oder extrem selten sind; max_df = 0.5 bedeutet, dass ein Wort in der Hälfte der Dokumente auftaucht (also vermutlich die Zielklassen nicht gut unterscheiden hilft). Außerdem können wir angeben, ob auf Grundlage von Wörtern oder von Zeichenketten (also Teilen von Wörtern) gesucht werden soll. Das hilft potentiell, verschiedene Wortformen zusammenzuführen (writing - write - written -> writ-…). Dieser Ansatz ist natürlich sehr grob; sauber wäre es, die Dokumente mit einem Lemmatisierer zu bearbeiten, der jeder Wortform ihre Grundform zuweist. Lemmatisierer sind im nltk, dem Natural Language Toolkit, verfügbar.

# Vektorisierer-Objekt anlegen

vectorizer = TfidfVectorizer(max_df=0.5, analyzer='word')

# andere mögliche Parameter wären max_df= 0.75 oder 1.0, analyzer = 'char'

Schritt 3b: Geeignete Features auswählen#

Wenn alle benötigten Features vorliegen, stellt sich die Frage, welche davon besonders relevant sind. Zum einen möchte man die Vorverarbeitungs- und Trainingszeiten gering halten, indem man mit möglichst wenig Features arbeitet. Zum anderen ist ein Modell mit wenig Features auch philosophisch besser: Es macht weniger Annahmen über die Welt und wird daher von Occam’s Razor präferiert: Es ist der einfachste Erklärungsansatz (also das Modell, das die wenigste Information benötigt) zu wählen. (Occam’s Razor eignet sich übrigens auch sehr gut zum Überprüfen von möglichen Verschwörungstheorien.)

Für die Feature-Auswahl gibt es viele Strategien:

Man kann die Features einzeln betrachten und z.B. Features ausschließen, die wenig Varianz zeigen (also für die meisten Datenpunkte gleich und damit nicht informativ sind).
Man kann die Features untereinander in Beziehung setzen und Features ausschließen, die stark mit anderen korreliert sind (deren Werte sich also aus anderen Features verlässlich vorhersagen lassen und die damit redundant sind).
Man kann ein vorläufiges Modell trainieren und die Feature-Wichtigkeit sozusagen aus der Praxis ableiten. Hierzu braucht man einen Lernalgorithmus, der Feature-Wichtigkeit ausgibt; es kann also grundsätzlich ein anderer Algorithmus sein als der eigentlich gewählte.

# Strategie 3: Linear SVC (lineare Support Vector Classification) gibt die Feature-Wichtigkeit aus. Parameter des
# modellbasierten Auswahlansatzes ist der Schwellwert, ab dem Features akzeptiert werden.

feature_selection = SelectFromModel(LinearSVC(penalty="l1", dual=False), threshold='mean')

# alternativer Parameter: threshold=None, es wird ein absoluter default-Schwellwert verwendet 

Schritt 4: Parameter des Algorithmus setzen#

Wir wählen als Algorithmus eine Support Vector Machine. Der für uns wichtigste Parameter ist der kernel (der die Abstandsberechnung der Datenpunkte bestimmt). Wir probieren den Standard-Radialkernel und zum Vergleich einen linearen Kernel aus.

Nun haben wir bereits an drei Stellen in unserem Prozess Parameter: Bei der Feature-Berechnung, bei der Feature-Auswahl und beim Algorithmus-Training selber. Die verschiedenen Parameter-Auswahlen können sich gegenseitig beeinflussen, es wäre also schön, alle Parameter zusammen zu evaluieren.

Wir können dies von Hand auf unseren oben erzeugten Entwicklungsdaten tun. Dafür brauchen wir 3 * 2 * 2 Evaluationsläufe (für die 3 Parameteroptionen des Vektorisierers und jeweils 2 Optionen der Feature-Auswahl und des Lerners).

# Lerner
classifier = SVC(kernel='linear')

# alternativer Parameter: kernel='rbf'


# Pipeline definieren -- die oben festgelegten Parameter werden verwendet

pipeline = Pipeline([('vectorizer', vectorizer), ('feature_selection', feature_selection),
                     ('classifier', classifier)])

# Pipeline auf 80% der Trainingsdaten laufen lassen
pipeline.fit(X_train, y_train)

# Vorhersage für 20% der Trainingsdaten (development-Daten) machen
dev_labels = pipeline.predict(X_dev)

# Evaluieren
#...

# noch 11x für die anderen Parameterkombinationen durchführen; Evaluationsergebnisse vergleichen

Dieser Ansatz funktioniert und ist sinnvoll, wenn Sie viele Trainingsdaten haben und wenig Parameter setzen müssen. Wenn wir aber einen Algorithmus austauschen oder neue Parameter(werte) bei den alten Ansätzen hinzufügen wollen, ist das aufwändig und fehleranfällig.

Wir verwenden deshalb stattdessen eine Pipeline und führen Grid Search auf allen Parameterkombinationen durch. Die Pipeline sorgt dafür, dass eine Reihe von Datentransformationen (Feature-Berechnung/Auswahl) automatisch durchgeführt und an einen Estimator (unseren Lerner) weitergegeben wird. Der Grid Search-Schritt führt eine Kreuzvalidierung auf den Trainingsdaten aus, die die Trainingsdaten (anders als unsere harte Aufteilung oben) optimal ausnutzt und genauso dafür sorgt, dass die Testdaten unangetastet bleiben können.

# Pipeline neu definieren - ohne Parametersetzen 

vectorizer = TfidfVectorizer()
feature_selection=SelectFromModel(LinearSVC(penalty="l1", dual=False))
classifier=SVC()

pipeline = Pipeline([('vectorizer', vectorizer), ('feature_selection', feature_selection),
                     ('classifier', classifier)])

# Parameterraum definieren: key ist schrittname__parametername, value die zu prüfenden Werte

parameters = {
    'vectorizer__max_df': (0.5, 0.75, 1.0), 
    'vectorizer__analyzer': ('word', 'char'),  
    'feature_selection__threshold': (None, 'mean'), 
    'classifier__kernel': ('linear','rbf')
}

# Suche über den gesamten Parameterraum (cross validation über die Trainingsdaten)
grid_search = GridSearchCV(pipeline, param_grid=parameters, verbose=10)

grid_search.fit(data_train['data'], data_train['target'])

Fitting 5 folds for each of 24 candidates, totalling 120 fits
[CV 1/5; 1/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5

[CV 1/5; 1/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5;, score=0.781 total time=   0.9s
[CV 2/5; 1/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5

[CV 2/5; 1/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5;, score=0.744 total time=   0.9s
[CV 3/5; 1/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5

[CV 3/5; 1/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5;, score=0.779 total time=   0.9s
[CV 4/5; 1/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5

[CV 4/5; 1/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5;, score=0.769 total time=   0.9s
[CV 5/5; 1/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5

[CV 5/5; 1/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.5;, score=0.768 total time=   0.9s
[CV 1/5; 2/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75

[CV 1/5; 2/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75;, score=0.786 total time=   1.0s
[CV 2/5; 2/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75

[CV 2/5; 2/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75;, score=0.737 total time=   1.3s
[CV 3/5; 2/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75

[CV 3/5; 2/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75;, score=0.767 total time=   1.3s
[CV 4/5; 2/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75

[CV 4/5; 2/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75;, score=0.769 total time=   1.2s
[CV 5/5; 2/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75

[CV 5/5; 2/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=0.75;, score=0.766 total time=   1.3s
[CV 1/5; 3/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0

[CV 1/5; 3/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0;, score=0.791 total time=   1.3s
[CV 2/5; 3/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0

[CV 2/5; 3/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0;, score=0.752 total time=   1.4s
[CV 3/5; 3/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0

[CV 3/5; 3/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0;, score=0.764 total time=   1.3s
[CV 4/5; 3/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0

[CV 4/5; 3/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0;, score=0.762 total time=   1.3s
[CV 5/5; 3/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0

[CV 5/5; 3/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=word, vectorizer__max_df=1.0;, score=0.773 total time=   1.3s
[CV 1/5; 4/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5

[CV 1/5; 4/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5;, score=0.455 total time=   0.5s
[CV 2/5; 4/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5

[CV 2/5; 4/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5;, score=0.425 total time=   0.5s
[CV 3/5; 4/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5

[CV 3/5; 4/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5;, score=0.428 total time=   0.6s
[CV 4/5; 4/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5

[CV 4/5; 4/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5;, score=0.420 total time=   0.6s
[CV 5/5; 4/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5

[CV 5/5; 4/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.5;, score=0.448 total time=   0.6s
[CV 1/5; 5/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75

[CV 1/5; 5/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75;, score=0.464 total time=   0.6s
[CV 2/5; 5/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75

[CV 2/5; 5/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75;, score=0.432 total time=   0.6s
[CV 3/5; 5/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75

[CV 3/5; 5/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75;, score=0.415 total time=   0.7s
[CV 4/5; 5/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75

[CV 4/5; 5/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75;, score=0.425 total time=   0.6s
[CV 5/5; 5/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75

[CV 5/5; 5/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=0.75;, score=0.458 total time=   0.7s
[CV 1/5; 6/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0

[CV 1/5; 6/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0;, score=0.474 total time=   1.0s
[CV 2/5; 6/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0

[CV 2/5; 6/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0;, score=0.486 total time=   1.1s
[CV 3/5; 6/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0

[CV 3/5; 6/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0;, score=0.491 total time=   1.1s
[CV 4/5; 6/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0

[CV 4/5; 6/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0;, score=0.479 total time=   1.0s
[CV 5/5; 6/24] START classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0

[CV 5/5; 6/24] END classifier__kernel=linear, feature_selection__threshold=None, vectorizer__analyzer=char, vectorizer__max_df=1.0;, score=0.441 total time=   1.0s
[CV 1/5; 7/24] START classifier__kernel=linear, feature_selection__threshold=mean, vectorizer__analyzer=word, vectorizer__max_df=0.5

[CV 1/5; 7/24] END classifier__kernel=linear, feature_selection__threshold=mean, vectorizer__analyzer=word, vectorizer__max_df=0.5;, score=0.786 total time=   1.1s
[CV 2/5; 7/24] START classifier__kernel=linear, feature_selection__threshold=mean, vectorizer__analyzer=word, vectorizer__max_df=0.5

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
/tmp/ipykernel_637/1550412393.py in <module>
     20 grid_search = GridSearchCV(pipeline, param_grid=parameters, verbose=10)
     21 
---> 22 grid_search.fit(data_train['data'], data_train['target'])

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/model_selection/_search.py in fit(self, X, y, groups, **fit_params)
    889                 return results
    890 
--> 891             self._run_search(evaluate_candidates)
    892 
    893             # multimetric is determined here because in the case of a callable

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/model_selection/_search.py in _run_search(self, evaluate_candidates)
   1390     def _run_search(self, evaluate_candidates):
   1391         """Search all candidates in param_grid"""
-> 1392         evaluate_candidates(ParameterGrid(self.param_grid))
   1393 
   1394 

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/model_selection/_search.py in evaluate_candidates(candidate_params, cv, more_results)
    849                     )
    850                     for (cand_idx, parameters), (split_idx, (train, test)) in product(
--> 851                         enumerate(candidate_params), enumerate(cv.split(X, y, groups))
    852                     )
    853                 )

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/joblib/parallel.py in __call__(self, iterable)
   1861             output = self._get_sequential_output(iterable)
   1862             next(output)
-> 1863             return output if self.return_generator else list(output)
   1864 
   1865         # Let's create an ID that uniquely identifies the current call. If the

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/joblib/parallel.py in _get_sequential_output(self, iterable)
   1790                 self.n_dispatched_batches += 1
   1791                 self.n_dispatched_tasks += 1
-> 1792                 res = func(*args, **kwargs)
   1793                 self.n_completed_tasks += 1
   1794                 self.print_progress()

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/utils/fixes.py in __call__(self, *args, **kwargs)
    214     def __call__(self, *args, **kwargs):
    215         with config_context(**self.config):
--> 216             return self.function(*args, **kwargs)
    217 
    218 

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/model_selection/_validation.py in _fit_and_score(estimator, X, y, scorer, train, test, verbose, parameters, fit_params, return_train_score, return_parameters, return_n_test_samples, return_times, return_estimator, split_progress, candidate_progress, error_score)
    678             estimator.fit(X_train, **fit_params)
    679         else:
--> 680             estimator.fit(X_train, y_train, **fit_params)
    681 
    682     except Exception:

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/pipeline.py in fit(self, X, y, **fit_params)
    392             if self._final_estimator != "passthrough":
    393                 fit_params_last_step = fit_params_steps[self.steps[-1][0]]
--> 394                 self._final_estimator.fit(Xt, y, **fit_params_last_step)
    395 
    396         return self

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/svm/_base.py in fit(self, X, y, sample_weight)
    253 
    254         seed = rnd.randint(np.iinfo("i").max)
--> 255         fit(X, y, sample_weight, solver_type, kernel, random_seed=seed)
    256         # see comment on the other call to np.iinfo in this file
    257 

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/svm/_base.py in _sparse_fit(self, X, y, sample_weight, solver_type, kernel, random_seed)
    374             int(self.probability),
    375             self.max_iter,
--> 376             random_seed,
    377         )
    378 

sklearn/svm/_libsvm_sparse.pyx in sklearn.svm._libsvm_sparse.libsvm_sparse_train()

/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/scipy/sparse/compressed.py in __init__(self, arg1, shape, dtype, copy)
     25     """base matrix class for compressed row- and column-oriented matrices"""
     26 
---> 27     def __init__(self, arg1, shape=None, dtype=None, copy=False):
     28         _data_matrix.__init__(self)
     29 

KeyboardInterrupt: 

Aufgabe: Warum führt das Grid Search 120 Läufe aus? Wir hatten doch 12 Parameterkombinationen ausgerechnet?

# Welche Parameterkombination ist die beste?

print(grid_search.best_estimator_)

# Wenn kein expliziter Parameter angegeben ist, hat der default am besten funktioniert.
# Wir wählen also 
#'vectorizer__max_df': 0.5 
# 'vectorizer__analyzer': 'word',  
# 'feature_selection__threshold': None, 
# 'classifier__kernel': 'rbf'

Pipeline(steps=[('vectorizer', TfidfVectorizer(max_df=0.5)),
                ('feature_selection',
                 SelectFromModel(estimator=LinearSVC(dual=False, penalty='l1'),
                                 threshold='mean')),
                ('classifier', SVC())])

# Pipeline für die beste Feature-Kombination definieren
final_pipeline = Pipeline(steps=[('vectorizer', TfidfVectorizer(max_df=0.5)),
                ('feature_selection',
                 SelectFromModel(estimator=LinearSVC(dual=False,
                                                     penalty='l1'),threshold='mean')),
                ('classifier', SVC())])

# Wie gut ist der fertige Lerner auf den Trainingsdaten? 
# Evaluation per Crossvalidation (analog zur Parametersuche)
# Mit cross_val_predict merken wir uns die Vorhersage für jeden Datenpunkt, die gemacht wird, wenn er zum Testset 
# gehört; die Vorhersagen sind also ungesehen und liegen für den gesamten Datensatz vor.

train_labels = cross_val_predict(final_pipeline, data_train['data'], data_train['target'], cv=10)

# Precision/Recall/F-Wert berechnen

print(classification_report(data_train['target'], train_labels))

              precision    recall  f1-score   support

           0       0.73      0.77      0.75       480
           1       0.91      0.89      0.90       584
           2       0.76      0.89      0.82       593
           3       0.79      0.54      0.64       377

    accuracy                           0.80      2034
   macro avg       0.80      0.77      0.78      2034
weighted avg       0.80      0.80      0.79      2034

Schritt 5: Vorhersagen auf Testdaten machen und evaluieren#

from sklearn.metrics import classification_report, confusion_matrix

# Jetzt den Lerner ein letztes Mal auf allen Trainingsdaten trainieren und dann auf den Testdaten evaluieren

# Lerner auf den gesamten Trainingsdaten trainieren
final_pipeline.fit(data_train['data'], data_train['target'])

# Lerner auf den Testdaten evaluieren

# Mit dem default score des Lerners: (durchschnittliche Accuracy bei SVC)

print("Default-Score des Klassifizierers: Accuracy=",final_pipeline.score(data_test['data'], data_test['target']), "\n")

# Labels vorhersagen lassen und dann Precision/Recall/F-Wert berechnen
test_labels = final_pipeline.predict(data_test['data'])

print(classification_report(data_test['target'], test_labels))

Default-Score des Klassifizierers: Accuracy= 0.7405764966740577 

              precision    recall  f1-score   support

           0       0.64      0.64      0.64       319
           1       0.86      0.84      0.85       389
           2       0.72      0.88      0.79       394
           3       0.70      0.50      0.58       251

    accuracy                           0.74      1353
   macro avg       0.73      0.71      0.72      1353
weighted avg       0.74      0.74      0.74      1353

Aufgabe: Interpretieren Sie die Ausgabe des Classification Report im Hinblick auf Precision, Recall und F-Score. Sie können die Konfusionsmatrix berechnen und zu Hilfe nehmen.

Welche Zielklasse ist am einfachsten zu lernen?
Wie hat sich das Ergebnis gegenüber den Trainingsdaten verändert?
Was bedeutet es, wenn die Precision höher ist als der Recall, oder umgekehrt?
Wenn Sie die Pipeline auf äquivalenten Daten produktiv einsetzen würden, wie viel Prozent falsche Vorhersagen sind zu erwarten?

Aufgabe:

Recherchieren Sie eine weitere Strategie zur Featurauswahl samt Parametern und setzen Sie sie in die Grid-Search-Pipeline ein. Vergleichen Sie dann unser bisheriges bestes Vorgehen und das neue beste Vorgehen. Sie dürfen auch gern mit anderen Pipeline-Schritten experimentieren.
Welches Risiko bringt es mit sich, wenn Sie Ihre Ergebnisse immer wieder auf den Testdaten vergleichen?