4. Dimensionalitätsreduktion#
Die Dimensionalität eines Datensatzes ist durch die Anzahl der vorliegenden Features gegeben. Es gibt verschiedene Motivationen, die Dimensionalität eines Datensatzes zu reduzieren:
Analyse und Visualisierung: Verstehen, welches die wichtigsten Features sind, und intuitivere Darstellung.
Effizienz: Trainings- und Testzeiten werden kürzer, wenn weniger (aber gleichermaßen aussagekräftige) Features verwendet werden.
Rauschen reduzieren: Features können falsch oder unvollständig belegt sein (das nennt man noisy oder verrauscht). Durch Dimensionsreduktion können Sie jeden Datenpunkt in Bezug auf einige wenige Dimensionen charakterisieren und das Rauschen teilweise ausgleichen.
Da bei der Dimensionalitätsreduktion immer (etwas) Information verloren geht, sollte man zunächst versuchen, ein Modell auf den Gesamtdaten zu trainieren, bevor man aus Grund 2 und 3 die Datendimensionalität verringert. Nur so kann man abschätzen, ob die schnellere Trainingszeit einen möglichen Performanzverlust aufwiegt bzw. ob die Rauschreduktion erfolgreich ist.
4.1. Lösungsansatz 1: Feature-Auswahl-Verfahren#
Der erste Lösungsansatz beruht darauf, aus der Menge der vorliegenden Features die geeignetsten auszuwählen. Es sollen also Features weggelassen werden, die wenig aussagefähig sind oder stark mit einem anderen Feature korrelieren (so dass sie praktisch dessen Information duplizieren). Solche redundanten Features können die Performanz mancher Lernalgorithmen sogar verschlechtern.
Wenn wir das Training eines spezifischen Lernalgorithmus verbessern und beschleunigen wollen, können wir auch die Features performanzbasiert so auswählen, dass der Algorithmus mit weniger Features besser oder zumindest nicht viel schlechter wird. Das haben Sie ja im vorherigen Kapitel “Klassifikation” schon gesehen. Hierzu brauchen wir natürlich Kreuzvalidierung oder einen speziellen Entwicklungs-Datensatz.
Aufgabe: Warum?
Dieses Verfahren eignet sich für Motivationen 1 und 2, weniger für 3 (da die potentiell verrauschten Originalfeatures ja beibehalten werden, nur nicht alle).
4.2. Lösungsansatz 2: Hauptkomponentenanalyse#
Das Feature-Auswahl-Verfahren betrachtet jede Dimension des Datensatzes einzeln. Die Hauptkomponentenanalyse/Prinicipal Components Analysis (PCA) betrachtet die Datenpunkte und ihre Lage im Raum als Ganzes.
Ziel des Verfahrens ist es, die Datenwolke auf eine niedrigerdimensionale Ebene herunterzuprojizieren, und zwar so, dass möglichst wenig der Varianz in den Daten verloren geht. Die Varianz der Daten stellt ja gerade die in ihnen vorhandene Information dar.
Man sucht also einige (wenige) Achsen, die die beste Projektionsebene beschreiben. Dies sind die Hauptkomponenten/Principal Components. Die erste Achse ist die, entlang der die Varianz des Datensatzes maximal ist. Die zweite Achse steht orthogonal zur ersten und maximiert die verbleibende Varianz des Datensatzes. Es können so viele Achsen gefunden werden, wie der Raum Dimensionen hat; allerdings erklären die Achsen zunehmend weniger Varianz.
Abb. 1 zeigt links drei mögliche Achsen für einen zweidimensionalen Datensatz. Das bedeutet, dass nicht alle Achsen paarweise orthogonal zueinander stehen. Nun ist die erste Hauptkomponente für den Datensatz zu wählen.
Rechts sieht man das Projektionsergebnis für jede der angedeuteten Linien (durchgezogen, gestrichelt, gepunktet). Die durchgezogene Linie (ganz oben) definiert offensichtlich die Projektionsebene, die die meiste Varianz bewahrt.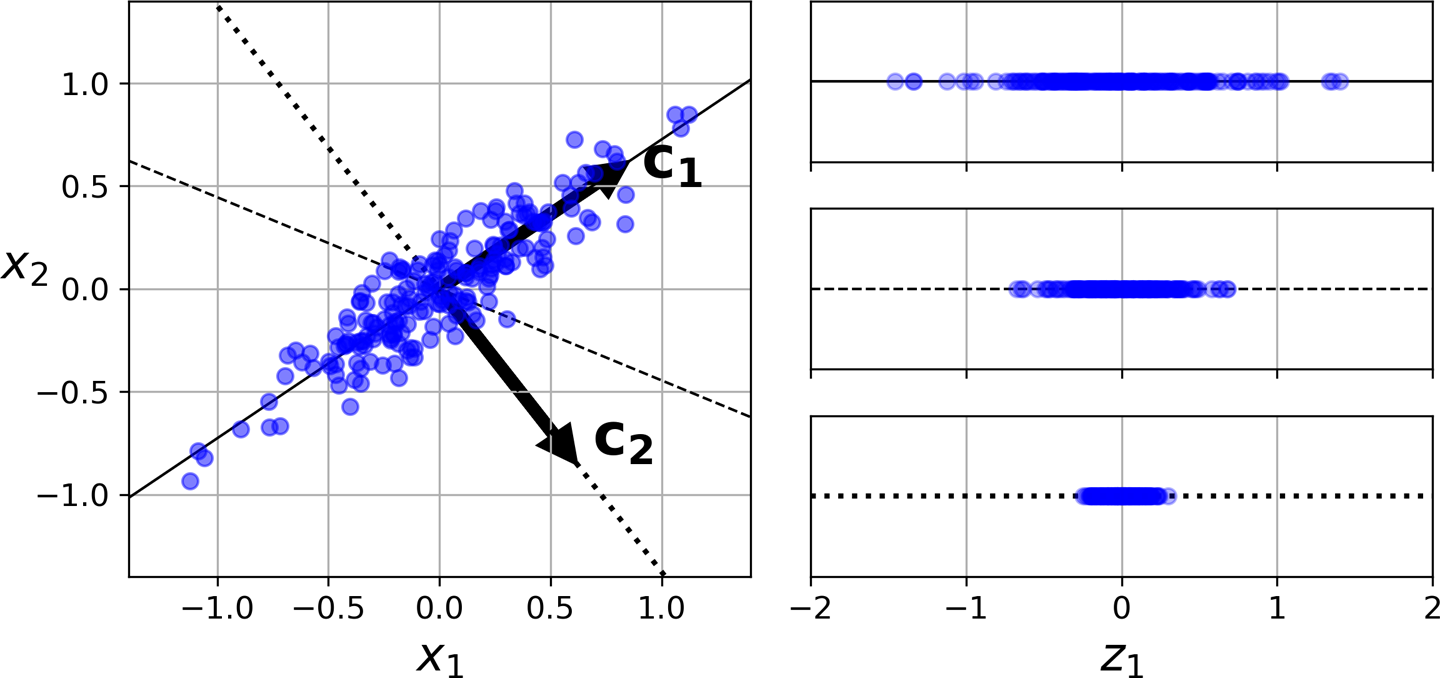 
Abb. 1: Mögliche Achsen für einen zweidimensionalen Datensatz und Projektion auf die Ebene, die jede Achse definiert. Aus: Géron (2019)
Aufgabe: Vollziehen Sie nach, warum genau die Achsen \(c_1\) und \(c_2\) als Hauptkomponenten gewählt werden müssen.
Wir nutzen nun nicht alle Hauptkomponenten (dann gäbe es ja keine Reduktion), sondern lassen einige der später gefundenen Hauptkomponenten weg. Da sie nicht mehr viel Varianz erklären, verlieren wir nicht viel Information. Die Daten werden auf die resultierende Ebene projiziert und durch die Dimensionen der Ebene repräsentiert. Das heißt, dass wir bei einer Datentransformation mit PCA nicht mehr unsere Ursprungsfeatures verwenden (in Abb. 1 werden Links Dimensionen \(x_1\) und \(x_2\) verwendet, rechts aber \(z_1\))!
PCA ist für alle Motivationen gut geeignet. Lerner werden mit weniger Features effizienter, und die Konzentration auf die aussagekräftigsten Hauptkomponenten reduziert irrelevante Varianz, entfernt also Rauschen. In der Analyse kann PCA Aufschluss darüber geben, wie die Varianz der Daten verteilt ist und welche Features gemeinsam variieren
In Python ist PCA als Transformer implementiert, kann also als Vorverarbeitungsschritt in eine Pipeline integriert werden. Wir können spezifizieren, wie viel Prozent der Ursprungsvarianz wir nach der Durchführung von PCA behalten wollen; dies definiert die Anzahl der verwendeten Hauptkomponenten. Je mehr Varianz wir abdecken wollen, desto geringer fällt die Dimensionsreduktion aus.
4.3. Lösungsansatz 3: Clustern#
Sie kennen das Clustern als ein unüberwachtes Klassifikationsverfahren zur Datenanalyse. Man kann es auch zur Dimensionsreduktion verwenden: Sie clustern Ihren Datensatz in n Cluster, und verwenden zukünftig als Features nur noch den Abstand jedes Datenpunkts zu den n Cluster-Zentroiden. Sie charakterisieren die Datenpunkte also nur noch durch ihre Nähe zu den Clustern. Dadurch haben Sie die Anzahl Ihrer Features auf n reduziert und vermutlich auch Rauschen in den Ursprungsfeatures reduziert. Der Ansatz eignet sich für alle drei Motivationen (da die Cluster ja zu Analysezwecken eingesetzt werden können).
4.4. Beispiel#
Wir führen alle drei Lösungsansätze für denselben Datensatz durch und vergleichen, ob und wie sich ein Klassifikationsalgorithmus dadurch verbessert. In der Praxis wählen Sie meist nur einen Lösungsansatz aus!
## Beispieldatensatz und SVM-Klassifikation von
# https://scikit-learn.org/stable/auto_examples/classification/plot_digits_classification.html#sphx-glr-auto-examples-classification-plot-digits-classification-py
# Aufgabe: Handgeschriebene Ziffern erkennen (also Klassifikation Bild -> Ziffer)
# Imports
from sklearn import datasets, svm, metrics
from sklearn.pipeline import Pipeline
from sklearn.feature_selection import VarianceThreshold
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import seaborn as sns
import matplotlib.pyplot as plt
# Daten laden
digits = datasets.load_digits()
# Die ersten vier Ziffern visualisieren
_, axes = plt.subplots(nrows=1, ncols=4, figsize=(10, 3))
for ax, image, label in zip(axes, digits.images, digits.target):
ax.set_axis_off()
ax.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
ax.set_title('Training: %i' % label)
# 8x8-Bilddarstellung in einen Vektor umformatieren
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
# Test- und Trainingsdaten einteilen
# Wir geben der Funktion train_test_split die Features und Zieldaten (X steht in sklearn für die Features,
# y für die Zieldaten) und spezifizieren, dass die Testdaten 50% des Datensatzes ausmachen sollten.
# Um die Aufteilung reproduzierbar (aber zufällig) zu machen, geben wir einen random state an. Bei einem neuen
# Aufruf mit demselben random state bekommen wir dieselbe Aufteilung
# Der Datensatz ist recht klein, daher sollten wir die zufällige Aufteilung stratifizieren:
# Aus jeder Zielklasse (=Originalziffer sollten ungefähr gleich viele Datenpunkte in Training und Test landen.
# Daher geben wir die Zielklassen als relevante Kategorien für die Stratifizierung an
X_train, X_test1, y_train, y_test1 = train_test_split(
data, digits.target, test_size=0.5, stratify=digits.target, random_state=42)
# Testdaten in Entwicklung und echten Test aufteilen (50-50, stratifiziert)
X_dev, X_test, y_dev, y_test = train_test_split(
X_test1, y_test1, test_size=0.5, stratify=y_test1, random_state=42)
# Klassifizierer vorbereiten: Support Vector Machine
clf = svm.SVC()
# Auf den Trainingsdaten lernen
clf.fit(X_train, y_train)
# Vorhersagen für die Testdaten machen und berichten
predicted = clf.predict(X_dev)
print(f"Classification report for classifier {clf}:\n"
f"{metrics.classification_report(y_dev, predicted)}\n")
Classification report for classifier SVC():
precision recall f1-score support
0 1.00 1.00 1.00 45
1 0.98 1.00 0.99 45
2 1.00 0.98 0.99 44
3 1.00 0.98 0.99 46
4 1.00 1.00 1.00 45
5 1.00 1.00 1.00 45
6 1.00 1.00 1.00 45
7 0.94 1.00 0.97 45
8 0.98 1.00 0.99 44
9 1.00 0.93 0.97 45
accuracy 0.99 449
macro avg 0.99 0.99 0.99 449
weighted avg 0.99 0.99 0.99 449
Lösungsansatz 1: Feature-Auswahl#
Die Strategie, Features spezifisch für den Lerner auszuwählen (SelectFromModel) kennen Sie bereits von letzter Woche. Daher hier eine ganz einfache Alternative: VarianceThreshold. Gibt es Features (= Pixel in den Bildern), die wenig Varianz zeigen, und die wir daher ignorieren können?
# Wie viel Varianz muss mindestens vorhanden sein?
dim_reduction = VarianceThreshold(0.1)
# Klassifizierer wählen
classifier = svm.SVC()
# Pipeline erstellen
pipeline = Pipeline([('dim_reduction', dim_reduction),
('classifier', classifier)])
pipeline.fit(X_train, y_train)
# Varianz der einzelnen Features ausgeben
# Hier können Sie sehen, welche Features bei Schwellenwert 0.1
# ausgefiltert werden.
print(dim_reduction.variances_)
[0.00000000e+00 7.92001280e-01 2.26409343e+01 1.88606865e+01
1.76214366e+01 3.18683241e+01 1.16142380e+01 1.07046716e+00
7.76409839e-03 1.00263292e+01 2.93975638e+01 1.67754537e+01
2.27688553e+01 3.67072051e+01 1.33423594e+01 6.98558043e-01
2.22221120e-03 1.29045156e+01 3.28851891e+01 3.38071934e+01
3.82638082e+01 3.90246985e+01 1.00352528e+01 1.99815477e-01
1.11234567e-03 9.79182271e+00 3.78508353e+01 3.55158655e+01
3.79406216e+01 3.43983475e+01 1.34165815e+01 2.22221120e-03
0.00000000e+00 1.18702784e+01 3.89458249e+01 3.89761063e+01
3.50106795e+01 3.36716137e+01 1.25370769e+01 0.00000000e+00
8.86404333e-03 8.89577061e+00 4.26853984e+01 4.15898594e+01
4.06724669e+01 3.18414157e+01 1.87615352e+01 8.73172752e-02
7.11901231e-02 3.13487532e+00 3.22770832e+01 2.75683615e+01
2.77509400e+01 3.66296459e+01 2.39021037e+01 7.57530965e-01
0.00000000e+00 8.33641698e-01 2.62217114e+01 1.97982909e+01
2.45886293e+01 3.52745237e+01 1.70264632e+01 2.83557621e+00]
Aufgabe: Identifizieren Sie einige Features, die ausgeschlossen werden. Fällt Ihnen etwas auf?
# Vorhersagen für die Testdaten machen und berichten
predicted = pipeline.predict(X_dev)
print(f"Classification report for VarianceThreshold dimensionality reduction:\n"
f"{metrics.classification_report(y_dev, predicted)}\n")
Classification report for VarianceThreshold dimensionality reduction:
precision recall f1-score support
0 1.00 1.00 1.00 45
1 0.98 1.00 0.99 45
2 1.00 0.98 0.99 44
3 1.00 0.98 0.99 46
4 1.00 1.00 1.00 45
5 1.00 1.00 1.00 45
6 1.00 1.00 1.00 45
7 0.94 1.00 0.97 45
8 0.98 1.00 0.99 44
9 1.00 0.93 0.97 45
accuracy 0.99 449
macro avg 0.99 0.99 0.99 449
weighted avg 0.99 0.99 0.99 449
Aufgabe: Haben wir unsere drei Ziele erreicht?
Lösungsansatz 2: PCA#
Können wir die Daten mit Hilfe von Hauptkomponenten komprimieren, ohne viel Information zu verlieren?
# PCA initialisieren; die Lösung soll mindestens 90% der Varianz in den Daten bewahren
dim_reduction = PCA(n_components=0.90)
# Klassifizierer wählen
classifier = svm.SVC()
# Pipeline erstellen
pipeline = Pipeline([('dim_reduction', dim_reduction),
('classifier', classifier)])
pipeline.fit(X_train, y_train)
# Ausgeben, wie viel Varianz die einzelnen Hauptkomponenten erklären.
print(dim_reduction.explained_variance_ratio_)
[0.14833813 0.13566403 0.11819438 0.09027783 0.05628636 0.04882407
0.04365129 0.03623729 0.03297623 0.03016733 0.02389832 0.02259636
0.01785772 0.01652811 0.01509009 0.0145833 0.01338468 0.012666
0.01035475 0.00910274 0.00847034]
Aufgabe:
Wie viele Hauptkomponenten werden verwendet, um 90% der Varianz zu erklären, wie viele Dimensionen sparen wir also ein?
Wie viele Dimensionen sind sehr aussagekräftig, wie viele sehr wenig aussagekräftig?
Die PCA liefert uns im Feld components_ die Hauptkomponenten als Achsen im Original-Feature-Raum. Hieran kann man sehen, welche Features für welche Hauptkomponente besonders wichtig sind.
# Visualisierung der Hauptkomponenten von
# https://charlesreid1.github.io/circe/Digit%20Classification%20-%20PCA.html
import seaborn as sns
fig = plt.figure(figsize=(10,8))
axes = [fig.add_subplot(220+i+1) for i in range(4)]
for i,ax in enumerate(axes):
sns.heatmap(dim_reduction.components_[i].reshape(8,8),
square=True, ax=ax,
vmax = 0.30, vmin=-0.30)
ax.set_title('Hauptkomponente '+str(i))
plt.show()
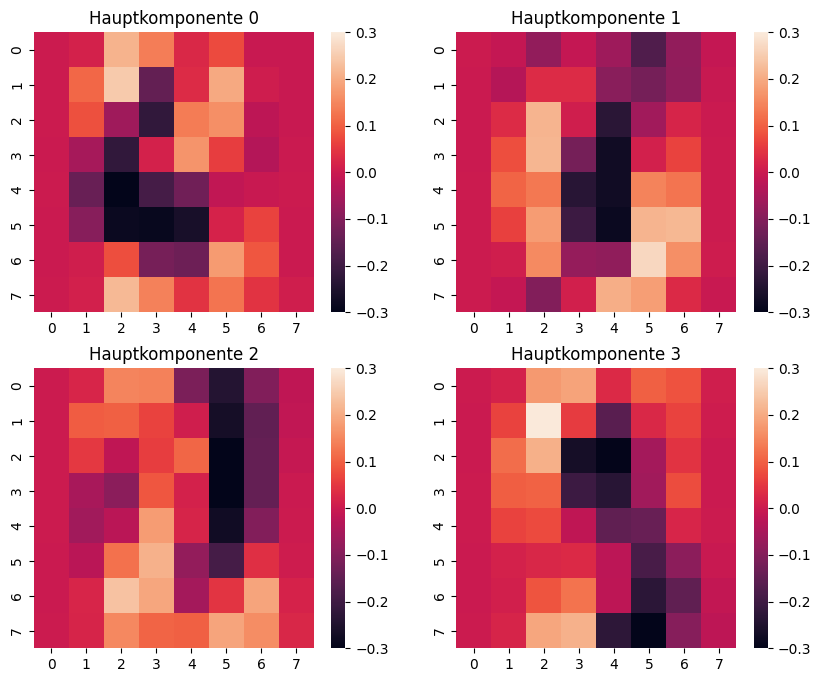
Aufgabe: Was sehen Sie?
# Vorhersagen für die Testdaten machen und berichten
predicted = pipeline.predict(X_dev)
print(f"Classification report for VarianceThreshold dimensionality reduction:\n"
f"{metrics.classification_report(y_dev, predicted)}\n")
Classification report for VarianceThreshold dimensionality reduction:
precision recall f1-score support
0 1.00 1.00 1.00 45
1 0.98 1.00 0.99 45
2 1.00 0.98 0.99 44
3 1.00 1.00 1.00 46
4 1.00 1.00 1.00 45
5 1.00 1.00 1.00 45
6 0.98 1.00 0.99 45
7 0.96 1.00 0.98 45
8 1.00 0.98 0.99 44
9 1.00 0.96 0.98 45
accuracy 0.99 449
macro avg 0.99 0.99 0.99 449
weighted avg 0.99 0.99 0.99 449
Aufgabe: Waren wir erfolgreich?
Lösungsansatz 3: Clustering#
Wir clustern die Bilddaten und beschreiben jedes Bild dann durch seine Distanz von den Cluster-Zentroiden.
# KMeans initialisieren: So viele Cluster wie Klassen
dim_reduction = KMeans(n_clusters=10, n_init=10)
# Klassifizierer wählen
classifier = svm.SVC()
# Pipeline erstellen; KMeans als Transformer führt die Cluster-basierte Dimensionsreduktion durch
pipeline = Pipeline([('dim_reduction', dim_reduction),
('classifier', classifier)])
pipeline.fit(X_train, y_train)
Pipeline(steps=[('dim_reduction', KMeans(n_clusters=10)),
('classifier', SVC())])
# Visualisierung der Zentroide von
# https://charlesreid1.github.io/circe/Digit%20Classification%20-%20PCA.html
fig = plt.figure(figsize=(20,10))
axes = [fig.add_subplot(2,5,0+i+1) for i in range(10)]
for i,ax in enumerate(axes):
sns.heatmap(dim_reduction.cluster_centers_[i].reshape(8,8),
square=True, ax=ax,
vmax = 1.0, vmin=0.0)
ax.set_title('Zentroid '+str(i))
plt.show()
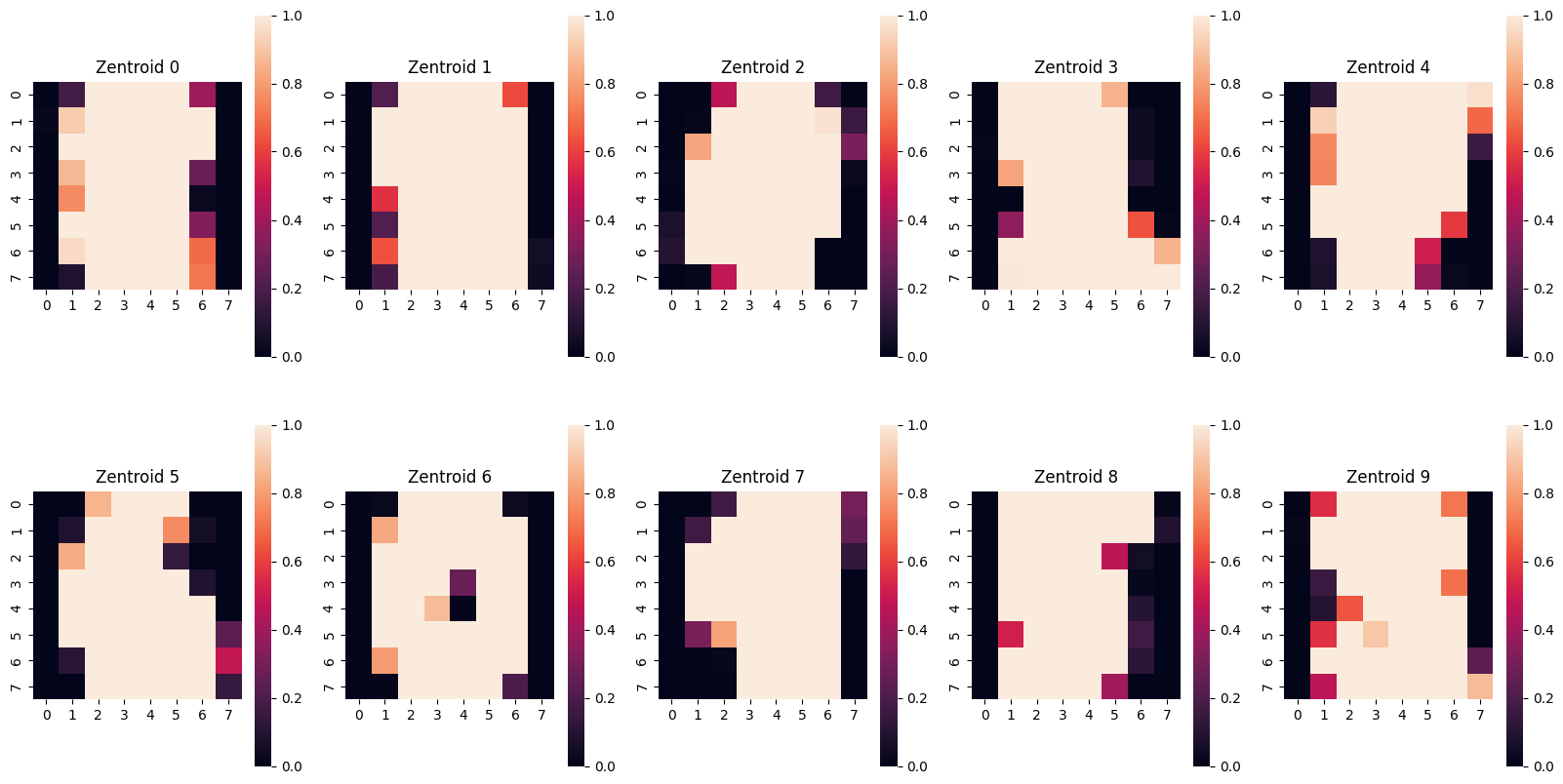
Die Visualisierung zeigt uns, dass 10 Cluster noch zu wenig sind - die Zentroide sehen alle sehr ähnlich aus.
# Vorhersagen für die Testdaten machen und berichten
predicted = pipeline.predict(X_dev)
print(f"Classification report for VarianceThreshold dimensionality reduction:\n"
f"{metrics.classification_report(y_dev, predicted)}\n")
Classification report for VarianceThreshold dimensionality reduction:
precision recall f1-score support
0 1.00 0.98 0.99 45
1 0.87 1.00 0.93 45
2 0.95 0.86 0.90 44
3 1.00 0.85 0.92 46
4 1.00 0.93 0.97 45
5 0.98 0.93 0.95 45
6 0.98 1.00 0.99 45
7 0.82 1.00 0.90 45
8 0.82 0.91 0.86 44
9 0.92 0.80 0.86 45
accuracy 0.93 449
macro avg 0.93 0.93 0.93 449
weighted avg 0.93 0.93 0.93 449
Aufgabe: Haben wir unser Ziel erreicht?
Aufgabe: Alle drei Algorithmen haben Parameter, die wir nicht optimiert haben. Wählen Sie einen Lösungsansatz und optimieren Sie die Parameter des Dimensionsreduktionsalgorithmus. Können Sie das Ergebnis weiter verbessern? Evaluieren Sie abschließend auf den ungesehenen Testdaten.