5. Regression#
Regressionsmodelle sagen konkrete, realwertige Zahlenwerte voraus. Wir betrachten das einfachste Regressionsmodell, das Ordinary Least Squares-Modell für lineare Regression.
Im Bereich der Data Analytics gibt es zwei Anwendungsformen für lineare Regression: Die Modellierung und die Prädiktion. Bei der Modellierung geht es darum, die Eigenschaften der Daten anhand des gelernten Modells besser zu verstehen. Man interpretiert also den Beitrag der einzelnen Features zum Modell und die Erklärmächtigkeit des Modells insgesamt. Dabei ist die Generalisierbarkeit auf neue Datenpunkte zweitrangig; deshalb arbeitet man bei diesem Ansatz durchaus von Anfang an auf dem gesamten Datensatz.
Die Prädiktion funktioniert wie bereits von der Klassifikation her bekannt: Auf den Trainingsdaten wird ein Modell trainiert und optimiert, und seine Generalisierbarkeit wird schließlich auf ungesehenen Testdaten geprüft. Wir brauchen natürlich gegenüber der Klassifikation neue Evaluationsmetriken, denn es gibt ja keine Zielklassen zum Vergleich für die Modell-Vorhersagen. Stattdessen basieren die Metriken auf der numerischen Abweichung zwischen Zielwert und vorhergesagtem Wert.
Im Code-Beispiel konzentrieren wir uns auf die Interpretation der gelernten Modelle und den Vergleich verschiedener Modelle auf Signifikanz ihrer Unterschiede hin.
In der Übung trainieren Sie ein prädiktives lineares Modell und evaluieren es durch Vergleich mit den Zielwerten der Testdaten.
5.1. 1. Lineare Regression#
Sie kennen das Prinzip der linearen Regression: Man modelliert einen Zielwert durch eine lineare Gleichung wie
\(y=w_0f_0 + w_1f_1 + ... + w_nf_n\)
Gleichung 1: Formel für die lineare Regression
Die \(f_n\) sind die Features des Datensatzes. Die Gewichte \(w_n\) heißen auch Koeffizienten. Hierbei ist \(f_0\) immer 1, denn \(w_0\) beschreibt das Interzept, den Achsenabschnitt, an dem die beschriebene Gerade die y-Achse schneidet.
Beim Training des Regressionsmodell werden die Gewichte \(w_0\) bis \(w_n\) gesetzt; dies ist ein Optimierungsproblem, das die Summe des quadrierten Fehlers (also der Abweichung zwischen Vorhersage und Zielwert) minimiert. Der Fehler wird quadriert, weil sich sonst positive und negative Abweichungen (also zu große und zu kleine Vorhersagen) gegenseitig aufheben würden. Vom quadrierten Fehler als zu minimierender Größe kommt der Name des Verfahrens, “(ordinary) least squares” (OLS).
Die Formel legt nahe, dass das Verfahren nur einsetzbar ist, wenn \(y\) sowie die \(f_n\) realwertige Zahlen sind. Das heißt, dass man Features mit anderem Typ vor dem Training aus dem Datensatz ausschließen muss. Im Notfall kann man sie auch numerisch umcodieren. Das ist aber problematisch, wenn die zu codierenden Klassen eigentlich keine natürliche Ordnung besitzen, da sie durch die Codierung ja eine bekommen. Durch dieses Hinzufügen von Information, die gar nicht in den Daten steckt, können Modellierungsfehler entstehen.
5.2. 2. Evaluationsmetrik: Root Mean Squared Error, RMSE#
Für die Evaluation wollen wir den Zielwert und vorhergesagten Wert vergleichen; aus dem Training kennen wir dafür noch die Summe des quadrierten Fehlers. Der Wert eignet sich aber noch nicht ideal, weil er von der Größe des Datensatzes abhängt. Daher teilt man durch \(N\), die Anzahl der Datenpunkte.
Der so entstehende MSE (mean squared error) hat aber noch die falsche Einheit - der Fehler wurde ja quadriert. Er gibt also nicht direkt Aufschluss darüber, wie groß die zu erwartende Abweichung für einen zukünftigen Datenpunkt sein wird. Daher ziehen wir wieder die Wurzel, um auf dieselbe Einheit zurückzukommen. Für den RMSE ergibt sich also die folgende Formel:
\(\sqrt{\frac{\sum_1^n{(exp_n - pred_n)^2}}{N}}\)
Gl. 2: Formel für den Root Mean Squared Error
Intuitiv besagt ein RMSE von 7, dass wir erwarten müssen, dass die Modellvorhersage durchschnittlich um 7 Punkte zu hoch oder zu tief sein wird. Ob das viel oder wenig ist, hängt von der beobachteten Durchschnittsgröße der Zielwerte ab; bei Zielwerten um 10 ist 7 sicher inakzeptabel, bei Zielwerten um 1000 ist die Vorhersage sehr genau.
5.3. 3. Training eines LR-Modells#
Wir haben in diesem Abschnitt das Ziel, die Daten zu modellieren und dadurch zu analysieren. Wir wollen nicht zukünftige Datenpunkte vorhersagen.
# Statsmodels ist mächtiger als das lineare Regressionsmodell in sklearn
#(insbesondere, was die Signifikanzberechnungen angeht)
# Installieren Sie statsmodels bei Bedarf mit Hilfe von pip statsmodels.api im Notebook.
import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# Daten laden: pandas dataframe
data = sm.datasets.fair.load_pandas().data
# Datenbeschreibung:
print(sm.datasets.fair.NOTE)
::
Number of observations: 6366
Number of variables: 9
Variable name definitions:
rate_marriage : How rate marriage, 1 = very poor, 2 = poor, 3 = fair,
4 = good, 5 = very good
age : Age
yrs_married : No. years married. Interval approximations. See
original paper for detailed explanation.
children : No. children
religious : How relgious, 1 = not, 2 = mildly, 3 = fairly,
4 = strongly
educ : Level of education, 9 = grade school, 12 = high
school, 14 = some college, 16 = college graduate,
17 = some graduate school, 20 = advanced degree
occupation : 1 = student, 2 = farming, agriculture; semi-skilled,
or unskilled worker; 3 = white-colloar; 4 = teacher
counselor social worker, nurse; artist, writers;
technician, skilled worker, 5 = managerial,
administrative, business, 6 = professional with
advanced degree
occupation_husb : Husband's occupation. Same as occupation.
affairs : measure of time spent in extramarital affairs
See the original paper for more details.
# Daten anschauen: Wir bekommen deskriptive Statistiken über die Daten
print(data.describe())
rate_marriage age yrs_married children religious \
count 6366.000000 6366.000000 6366.000000 6366.000000 6366.000000
mean 4.109645 29.082862 9.009425 1.396874 2.426170
std 0.961430 6.847882 7.280120 1.433471 0.878369
min 1.000000 17.500000 0.500000 0.000000 1.000000
25% 4.000000 22.000000 2.500000 0.000000 2.000000
50% 4.000000 27.000000 6.000000 1.000000 2.000000
75% 5.000000 32.000000 16.500000 2.000000 3.000000
max 5.000000 42.000000 23.000000 5.500000 4.000000
educ occupation occupation_husb affairs
count 6366.000000 6366.000000 6366.000000 6366.000000
mean 14.209865 3.424128 3.850141 0.705374
std 2.178003 0.942399 1.346435 2.203374
min 9.000000 1.000000 1.000000 0.000000
25% 12.000000 3.000000 3.000000 0.000000
50% 14.000000 3.000000 4.000000 0.000000
75% 16.000000 4.000000 5.000000 0.484848
max 20.000000 6.000000 6.000000 57.599991
Aufgabe: Interpretieren Sie die deskriptive Statistik.
Sind die meisten der Befragten in ihren Ehen glücklich oder unglücklich?
Haben die meisten der Befragten eine Affäre (gehabt) oder nicht?
Waren die Affären eher lang oder eher kurz?
Beim Betrachten der Daten fällt ein extremer Datenpunkt auf, den wir bereinigen wollen.
# Welcher Datenpunkt hat den extrem hohen Wert für 'affairs'?
print(data.index[data['affairs'] >57.5].tolist())
print (data.loc[[749]])
# Löschen
data.drop(labels=[749],axis=0, inplace=True)
[749]
rate_marriage age yrs_married children religious educ occupation \
749 5.0 22.0 2.5 1.0 1.0 14.0 3.0
occupation_husb affairs
749 5.0 57.599991
# Daten wieder anschauen: Besser! Die Aussagen von oben stimmen aber grundsätzlich noch.
print(data.describe())
rate_marriage age yrs_married children religious \
count 6365.000000 6365.000000 6365.000000 6365.000000 6365.000000
mean 4.109505 29.083975 9.010448 1.396936 2.426394
std 0.961440 6.847844 7.280235 1.433575 0.878256
min 1.000000 17.500000 0.500000 0.000000 1.000000
25% 4.000000 22.000000 2.500000 0.000000 2.000000
50% 4.000000 27.000000 6.000000 1.000000 2.000000
75% 5.000000 32.000000 16.500000 2.000000 3.000000
max 5.000000 42.000000 23.000000 5.500000 4.000000
educ occupation occupation_husb affairs
count 6365.000000 6365.000000 6365.000000 6365.000000
mean 14.209898 3.424195 3.849961 0.696435
std 2.178172 0.942458 1.346464 2.084921
min 9.000000 1.000000 1.000000 0.000000
25% 12.000000 3.000000 3.000000 0.000000
50% 14.000000 3.000000 4.000000 0.000000
75% 16.000000 4.000000 5.000000 0.484848
max 20.000000 6.000000 6.000000 39.199982
5.4. 4. Interpretation eines LR-Modells#
Aus der Analysesicht kann man entweder mit einem Modell beginnen, das alle Features enthält, und es dann schrittweise verfeinern, oder man beginnt mit einem künstlich einfachen Modell als Vergleichspunkt.
Wir beginnen so herum und trainieren zuerst ein einfaches Modell, dessen Attribute wir theoretisch motiviert auswählen: Wir treffen die Annahme, dass glücklich Verheiratete weniger Affären haben.
# Syntax für die Regressionsgleichung: Zielwert ~ Feature 1 + Feature 2 + ...
affair_basic = ols("affairs ~ rate_marriage ", data).fit()
print(affair_basic.summary())
OLS Regression Results
==============================================================================
Dep. Variable: affairs R-squared: 0.037
Model: OLS Adj. R-squared: 0.037
Method: Least Squares F-statistic: 244.0
Date: Thu, 02 Oct 2025 Prob (F-statistic): 5.19e-54
Time: 13:17:22 Log-Likelihood: -13588.
No. Observations: 6365 AIC: 2.718e+04
Df Residuals: 6363 BIC: 2.719e+04
Df Model: 1
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
Intercept 2.4091 0.113 21.396 0.000 2.188 2.630
rate_marriage -0.4168 0.027 -15.621 0.000 -0.469 -0.364
==============================================================================
Omnibus: 8248.132 Durbin-Watson: 1.635
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1745099.744
Skew: 7.189 Prob(JB): 0.00
Kurtosis: 82.833 Cond. No. 19.5
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Die Ausgabe mit Informationen über das Modell gibt uns einige sehr wichtige Anhaltspunkte zur Qualität des Modells.
Zum einen sehen wir oben rechts den R-squared-Wert. Er wird berechnet, indem die Zielwerte und Vorhersagen des Modells (für die Trainingsdaten!!) korreliert werden; dies ergibt Pearson’s r für die Korrelation. Dieser Wert wird dann noch quadriert. R-squared gibt an, welcher Anteil der Varianz in den Zieldaten von den Modellvorhersagen erklärt werden kann. Bei unserem Modell ist das eher wenig: R-squared = 0.037, also war die Korrelation r=0.19, was eine schwache Beziehung beschreibt. Wir würden gern Werte von 0.36 aufwärts sehen; Korrelationen gelten ab r=0.6 als “stark”.
Zum zweiten listet die Übersicht die Koeffizienten des Modells auf. Es gibt neben dem Intercept, also dem konstanten Gleichungsfaktor, für jeden Modellterm einen - bei uns also für rate_marriage als einzigem Modellterm. Der numerische Wert des Koeffizienten erlaubt keinen Rückschluss auf die Wichtigkeit des Koeffizienten, weil der Koeffizient ja mit den Werten des Modellterms multipliziert wird, um den Zielwert vorherzusagen. Modellterme mit durchschnittlich großen Eingabewerten haben also immer numerisch kleinere Koeffizienten als Modellterme mit durchschnittlich kleineren Eingabewerten, wenn die Vorhersagekraft ähnlich ist.
Um zu bewerten, ob ein Modellterm für das Modell wichtig ist, betrachtet wir den p-Wert des Koeffizienten (Spalte P>|t|). Für jeden Koeffizienten wird die Nullhypothese getestet, dass er eigentlich äquivalent zu 0 ist (also keine Auswirkung hat). Ist der p-Wert dieses Tests unter 0.05, kann die Hypothese verworfen werden und der Koeffizient bzw. der Modellterm ist bedeutungsvoll. Das ist bei unserem Term der Fall.
Interessant ist auch das Vorzeichen des Koeffizienten. Ein positiver Koeffizient beschreibt eine positive Beziehung zwischen Modellterm und Zielwert: Sie wachsen und schrumpfen gemeinsam. Ein negativer Koeffizient, wie in unserem Fall, beschreibt eine negative Beziehung: Wächst der Modellterm, sinkt der Zielwert und umgekehrt. Das entspricht unserer Annahme für unseren Modellterm: Je glücklicher eine Ehe bewertet wird, desto weniger Zeit verbrachte die Ehefrau in einer Affäre.
Aus dem konkreten numerischen Wert jedes Koeffizienten erkennen wir, wie sich der Zielwert für eine schrittweise Veränderung des Eingabewerts verändern wird. In unserem Beispiel entspricht eine um 1 höhere Bewertung der Ehe einer Verkürzung der vorhergesagten Affärenlänge um -0.42 (-0.42 * 1). (Wenn mehrere Modellterme vorliegen, gilt diese Veränderung nur, wenn die Eingabewerte der anderen Modellterme konstant bleiben.)
Ein Beispiel: Für jeden Datenpunkt wird zunächst der Koeffizient des Intercepts als Affärenlänge vorhergesagt (also 2.4 Zeiteinheiten). Für eine glücklich verheiratete Frau wird nun 5*-0.42 = -2.1 hinzuaddiert. Die finale Vorhersage ist also eine Affärendauer von 0.3 Zeiteinheiten, wenn die Ehe als maximal glücklich beschrieben wird. (Dies erklärt auch den schlechten Erklärwert unseres Modells - das ist angesichts der deskriptiven Statistik oben vermutlich zu hoch.)
5.5. 4. Vergleich zweier LR-Modelle#
Unser bisheriges Modell war extrem einfach und hat die Mehrzahl der verfügbaren Features außer Acht gelassen. Wir trainieren also jetzt ein Modell mit allen Attributen und vergleichen die beiden.
# Jetzt ein komplizierteres Modell mit allen verfügbaren Attributen.
affair_full = ols("affairs ~ rate_marriage + age + yrs_married + children"
" + religious + educ + occupation + occupation_husb", data).fit()
print(affair_full.summary())
OLS Regression Results
==============================================================================
Dep. Variable: affairs R-squared: 0.061
Model: OLS Adj. R-squared: 0.059
Method: Least Squares F-statistic: 51.28
Date: Thu, 02 Oct 2025 Prob (F-statistic): 5.81e-81
Time: 13:17:22 Log-Likelihood: -13509.
No. Observations: 6365 AIC: 2.704e+04
Df Residuals: 6356 BIC: 2.710e+04
Df Model: 8
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 3.5876 0.251 14.302 0.000 3.096 4.079
rate_marriage -0.4298 0.027 -16.026 0.000 -0.482 -0.377
age -0.0132 0.009 -1.531 0.126 -0.030 0.004
yrs_married -0.0152 0.009 -1.630 0.103 -0.033 0.003
children -0.0245 0.028 -0.870 0.384 -0.080 0.031
religious -0.2272 0.029 -7.731 0.000 -0.285 -0.170
educ -0.0174 0.013 -1.312 0.189 -0.043 0.009
occupation 0.0704 0.030 2.383 0.017 0.012 0.128
occupation_husb -0.0031 0.020 -0.160 0.873 -0.042 0.035
==============================================================================
Omnibus: 8151.163 Durbin-Watson: 1.624
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1686531.877
Skew: 7.034 Prob(JB): 0.00
Kurtosis: 81.494 Cond. No. 349.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Aufgabe: Interpretieren Sie die Modellausgabe.
Erklärt das Modell jetzt mehr Varianz? Viel mehr?
Welche Features/Modellterme sind für das Modell relevant, haben also einen signifikaten Koeffizienten?
In welche Richtung nehmen diese Features Einfluss auf die Zielwerte?
Wir trainieren ein optimiertes Modell nur mit den relevanten Koeffizienten. Wenn ‘rate_marriage’, ‘religious’ und ‘occupation’ verwendet werden, ist ‘occupation’ nicht mehr signifikant; wir lassen es daher auch weg:
affair_opt = ols("affairs ~ rate_marriage"
" + religious", data).fit()
print(affair_opt.summary())
OLS Regression Results
==============================================================================
Dep. Variable: affairs R-squared: 0.049
Model: OLS Adj. R-squared: 0.049
Method: Least Squares F-statistic: 165.0
Date: Thu, 02 Oct 2025 Prob (F-statistic): 1.31e-70
Time: 13:17:22 Log-Likelihood: -13547.
No. Observations: 6365 AIC: 2.710e+04
Df Residuals: 6362 BIC: 2.712e+04
Df Model: 2
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
Intercept 2.9737 0.128 23.249 0.000 2.723 3.224
rate_marriage -0.3976 0.027 -14.953 0.000 -0.450 -0.345
religious -0.2651 0.029 -9.106 0.000 -0.322 -0.208
==============================================================================
Omnibus: 8210.508 Durbin-Watson: 1.648
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1716680.292
Skew: 7.130 Prob(JB): 0.00
Kurtosis: 82.181 Cond. No. 25.4
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Beim resultierenden Modell ist R-squared wieder schlechter als beim vollen Modell, aber es ist noch besser als unser einfachstes Modell. Gemessen an R-squared ist also affair_full > affair_opt > affair_basic.
Modellvergleich mit ANOVA#
Aber ist dieser Unterschied aussagekräftig, oder sind die Modelle so nah zusammen, dass der numerische Unterschied egal ist?
Wir führen eine ANOVA (ANalysis Of VAriance, Varianzanalyse) auf der Varianz der Vorhersagefehler der Modelle durch. Ist die ANOVA signifikant, unterscheiden sich die Modelle deutlich. Wenn nicht, sind sie äquivalent.
anova_results = anova_lm(affair_basic, affair_opt, affair_full)
print('\nANOVA results')
print(anova_results)
ANOVA results
df_resid ssr df_diff ss_diff F Pr(>F)
0 6363.0 26641.904003 0.0 NaN NaN NaN
1 6362.0 26299.107935 1.0 342.796068 83.843955 7.086653e-20
2 6356.0 25986.510449 6.0 312.597486 12.742955 2.360256e-14
Der Aufruf von anova_lm vergleicht jedes Modell mit dem Vorhergehenden. Die Modelle werden also in der Reihenfolge angegeben, wie wir sie vergleichen wollen: Nach unseren bisherigen Ergebnissen wollen wir wissen, ob affair_opt nur numerisch oder wirklich signifikant besser als affair_basic und schlechter als affair_full ist. Die erste Ausgabezeile ist für uns egal, weil für affair_basic kein Vorgänger vorhanden ist.
Sowohl der Vergleich von affair_opt mit affair_basic als auch der Vergleich von affair_full mit affair_opt ist signifikant (s. Spalte PR(<F), die den ermittelten P-Wert des Vergleichs anzeigt; Werte kleiner 0.05 weisen auf Signifikanz hin); affair_full ist also tatsächlich besser als affair_opt (und damit auch als affair_basic).
Wir lernen also aus dieser Modellierung: Die Daten sind sehr schwierig mit einem linearen Modell zu fassen. Eventuell liegt ein nicht-linearer Zusammenhang vor (dies können Sie durch Plotten der Daten überprüfen, wenn Sie möchten). Die beiden wichtigsten Faktoren waren, wie glücklich verheiratet und wie religiös die Befragten waren; je mehr beides der Fall ist, desto weniger wahrscheinlich ist eine Affäre. Um die Daten optimal abzubilden, sollten jedoch alle vorhandenen Faktoren einbezogen werden; das so entstehende Modell erklärt signifikant mehr Varianz in den Daten als ein Modell nur mit den beiden wichtigsten Faktoren.
5.6. 5. Aufgabe: Vorhersage ungesehener Daten#
Sie können natürlich mit linearer Regression auch prädiktive Modelle bauen. Dann teilen Sie wie üblich die Daten in 2-3 Teildatensätze auf, trainieren und optimieren auf den Trainings- und Entwicklungsdaten und sagen dann die Testdaten voraus. Die Evaluation geschieht dann mit Hilfe von Metriken wie RMSE.
Probieren Sie es aus - diesmal mit sklearn und der Vorgehensweise des Maschinellen Lernens. Wir verwenden den California-Housing-Datensatz (z.B. https://scipy-lectures.org/packages/scikit-learn/auto_examples/plot_california_prediction.html).
# Imports
from sklearn.datasets import fetch_california_housing
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import root_mean_squared_error as RMSE
---------------------------------------------------------------------------
ImportError Traceback (most recent call last)
/tmp/ipykernel_928/1728772773.py in <module>
5 from sklearn.model_selection import train_test_split
6 from sklearn.linear_model import LinearRegression
----> 7 from sklearn.metrics import root_mean_squared_error as RMSE
ImportError: cannot import name 'root_mean_squared_error' from 'sklearn.metrics' (/builds/speiser/vl-data-analytics/venv/lib/python3.7/site-packages/sklearn/metrics/__init__.py)
Laden Sie die Daten und plotten Sie die Features gegen den Zielwert (Price), um sich einen Eindruck von der Datenverteilung zu machen.
# Daten laden
data = fetch_california_housing(as_frame=True)
# Beschreibung drucken
print(data.DESCR)
.. _california_housing_dataset:
California Housing dataset
--------------------------
**Data Set Characteristics:**
:Number of Instances: 20640
:Number of Attributes: 8 numeric, predictive attributes and the target
:Attribute Information:
- MedInc median income in block group
- HouseAge median house age in block group
- AveRooms average number of rooms per household
- AveBedrms average number of bedrooms per household
- Population block group population
- AveOccup average number of household members
- Latitude block group latitude
- Longitude block group longitude
:Missing Attribute Values: None
This dataset was obtained from the StatLib repository.
https://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.html
The target variable is the median house value for California districts,
expressed in hundreds of thousands of dollars ($100,000).
This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).
A household is a group of people residing within a home. Since the average
number of rooms and bedrooms in this dataset are provided per household, these
columns may take surprisingly large values for block groups with few households
and many empty houses, such as vacation resorts.
It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.
.. topic:: References
- Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
Statistics and Probability Letters, 33 (1997) 291-297
# Daten gegen Zielwert (Preis) plotten
plt.figure(figsize=(4, 3))
plt.hist(data.target)
plt.xlabel('price ($1000s)')
plt.ylabel('count')
plt.tight_layout()
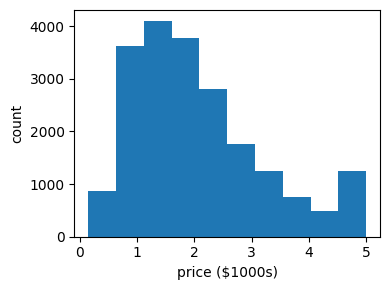
Teilen Sie die Daten in Training-Entwicklung-Test auf.
# Wie ist die Struktur?
# print(data)
# Beobachtung: Es gibt einmal die Features (data.data) und einmal die Zielvariable (data.target)
# Daten aufteilen: Testdaten
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)
# Nicht-Testdaten weiter aufteilen: Training und Entwicklung
X_train, X_dev, y_train, y_dev = train_test_split(X_train, y_train)
print(len(X_train), len(X_dev), len(X_test))
11610 3870 5160
Trainieren Sie mit sklearn.linearModel.LinearRegression ein Modell und betrachten Sie die Koeffizienten.
# Modell trainieren
clf = LinearRegression()
clf.fit(X_train, y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
Fragen:
Welche Features beeinflussen den Preis negativ?
Welchen Unterschied im Preis macht es, wenn ein sonst gleiches Haus ein Schlafzimmer mehr hat als ein anderes?
print(clf.intercept_, clf.coef_)
-36.7701372442047 [ 4.42961153e-01 1.01038057e-02 -1.16521002e-01 7.37478676e-01
-9.46902054e-07 -6.31574731e-03 -4.24300975e-01 -4.33260613e-01]
Evaluieren Sie Ihr Modell auf den Entwicklungsdaten. Verwenden Sie den RMSE und R-squared.
# Vorhersage machen und evaluieren
predicted = clf.predict(X_dev)
expected = y_dev
print("RMSE: ")
RMSE(expected, predicted)
RMSE:
0.536138713204159
Möglicherweise haben nicht alle Features eine lineare Beziehung zum Preis. Dies können wir annähern, indem wir mit der Methode sklearn.preprocessing.PolynomialFeatures zusätzlich zu jedem Ausgangsfeature auch sein Quadrat und für die Summe mit jedem anderen Feature berechnen. Damit decken wir auch quadratische Abhängigkeiten und Feature-Kombinationen ab (ähnlich wie ein polynomieller Kernel beim SVM). Die berechnete Regressionsgleichung bleibt aber linear!
Probieren Sie aus, ob diese Feature-Transformation für die California-Housing-Daten nützlich ist (Evaluation auf den Entwicklungsdaten).
from sklearn.preprocessing import PolynomialFeatures
# Nichtlinearer Anteil in den Features: PolynomialFeatures
poly = PolynomialFeatures(2)
X_train_polynom = poly.fit_transform(X_train)
X_dev_polynom = poly.fit_transform(X_dev)
# Modell mit polynomiellen Features trainieren
clf.fit(X_train_polynom, y_train)
# Evaluation auf den Entwicklungsdaten
predicted = clf.predict(X_dev_polynom)
expected = y_dev
print("RMSE: ")
RMSE(expected, predicted)
RMSE:
0.5367008257682664
Wir haben bei der Analyse der Daten kaum die Dateneigenschaften angeschaut. Eventuell haben wir Probleme mit dem Datensatz übersehen. Plotten Sie deshalb alle Features gegen die Zielvariable, und lassen Sie sich die deskriptive Statistik der Features ausgeben (data.describe()). Fallen Ihnen Probleme auf?
Eine schöne Übersicht über die mögliche tiefergehende Datenanalyse und eine Strategie zum Verbessern der Ergebnisse finden sie unter https://inria.github.io/scikit-learn-mooc/python_scripts/datasets_california_housing.html
